Difference between revisions of "Annihilation of calcium oscillations with PLC activation inhibition"
From mintOC
m |
|||
| Line 31: | Line 31: | ||
== Reference Solutions == | == Reference Solutions == | ||
| − | A solution for this problem is described in <bibref>Lebiedz2005</bibref>. | + | A solution for this problem is described in <bibref>Lebiedz2005</bibref>. A local minimum that is actually slightly worse than the solution provided for only one control, is shown in the next plots. |
| + | |||
| + | [[Image:calcium2Controls.png]] [[Image:calcium2States.png]] | ||
| + | <gallery caption="Reference solution plots" widths="180px" heights="140px" perrow="2"> | ||
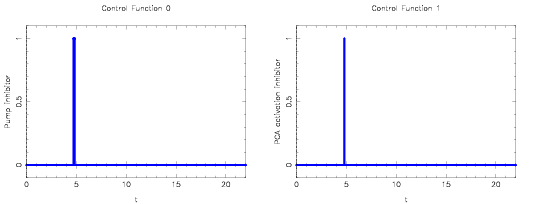
| + | Image:calcium2Controls.png| Optimal stimuli determined by mixed-integer optimal control. | ||
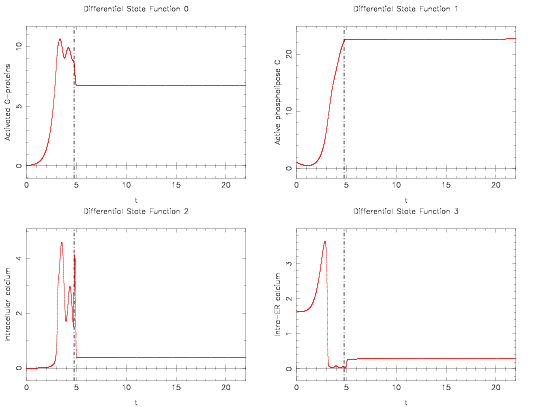
| + | Image:calcium2States.png| Corresponding differential states. | ||
| + | </gallery> | ||
== Variants == | == Variants == | ||
Revision as of 22:26, 12 November 2008
| Annihilation of calcium oscillations with PLC activation inhibition | |
|---|---|
| State dimension: | 1 |
| Differential states: | 4 |
| Discrete control functions: | 2 |
| Interior point equalities: | 4 |
This control problem is closely related to Annihilation of calcium oscillations. The only difference is an additional control function, the inhibition of PLC activation. We state only the differences in this article.
Mathematical formulation
For ![t \in [t_0, t_f]](https://mintoc.de/images/math/5/5/8/55823791d9100bcb5461801aff4f6edd.png)
almost everywhere the mixed-integer optimal control problem is given by
![\begin{array}{llcl}
\displaystyle \min_{x, w, w^{\mathrm{max}}} & & & {\int_{t_0}^{t_f} || x(\tau) - \tilde{x} ||_2^2 + p_1 w_1(\tau) + p_2 w_2(\tau) \; \mathrm{d}\tau} \\[1.5ex]
\mbox{s.t.} & \dot{x}_0 & = & k_1 + k_2 x_0 - \frac{k_3 x_0 x_1}{x_0 + K_4} - \frac{k_5 x_0 x_2}{x_0 + K_6} \\
& \dot{x}_1 & = & (1 - w_2) k_7 x_0 - \frac{k_8 x_1}{x_1 + K_9} \\
& \dot{x}_2 & = & \frac{k_{10} x_1 x_2 x_3}{x_3 + K_{11}} + k_{12} x_1 + k_{13} x_0 - \frac{k_{14} x_2}{w_1 \cdot x_2 + K_{15}} - \frac{k_{16} x_2}{x_2 + K_{17}} + \frac{x_3}{10} \\
& \dot{x}_3 & = & - \frac{k_{10} x_1 x_2 x_3}{x_3 + K_{11}} + \frac{k_{16} x_2}{x_2 + K_{17}} - \frac{x_3}{10} \\[1.5ex]
& x(0) &=& (0.03966, 1.09799, 0.00142, 1.65431)^T, \\
& x(t) & \ge & 0.0, \\
& w(t) &\in& \{0, w^{\mathrm{max}}\}, \\
& w^{\mathrm{max}} & \ge & 1.1, \\
& w^{\mathrm{max}} & \le & 1.3.
\end{array}](https://mintoc.de/images/math/4/a/d/4ad9919a6127fe156223482b7202f11c.png)
Note that we write 
instead of 
and have an additional control function 
. The regularization parameters are set to 
.
Reference Solutions
A solution for this problem is described in <bibref>Lebiedz2005</bibref>. A local minimum that is actually slightly worse than the solution provided for only one control, is shown in the next plots.
- Reference solution plots
Optimal stimuli determined by mixed-integer optimal control.
Corresponding differential states.
Variants
References
<bibreferences/>
