Category:Hyperbolic
From mintOC
Revision as of 16:24, 24 February 2016 by FelixMueller (Talk | contribs)
This category contains all control problems which are governed by a hyperbolic partial differential equation.
A second order linear partial differential equation can be written as
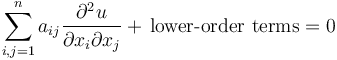 .
.
If the matrix 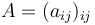 is indefinite such that
is indefinite such that 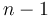 eigenvalues have the same sign and the remaining eigenvalue has the other sign, the partial differential equation is called hyperbolic.
eigenvalues have the same sign and the remaining eigenvalue has the other sign, the partial differential equation is called hyperbolic.
An example is the wave equation: 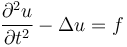 ,
where
,
where  denotes the Laplace operator,
denotes the Laplace operator, 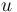 is the unknown, and the function
is the unknown, and the function 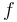 is given.
is given.
Pages in category "Hyperbolic"
This category contains only the following page.