Diels-Alder Reaction Experimental Design

This page can now be filled with content.

Model Formulation

Differential equation system:

$\begin{array}{rcl} \dot{n_1}(t) &=& -k \cdot \frac{n_1(t) \ \cdot \ n_2(t)}{m_{tot}}, \\ & & \\ \dot{n_2}(t) &=& -k \cdot \frac{n_1(t) \ \cdot \ n_2(t)}{m_{tot}}, \\ & & \\ \dot{n_2}(t) &=& \ \ k \cdot \frac{n_1(t) \ \cdot \ n_2(t)}{m_{tot}} \end{array}$

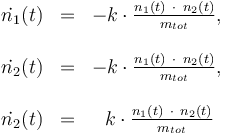
Reaction velocity constant:

$k = k_1 \ \cdot \ exp(- \frac{E_1}{R} \ \cdot \ (\frac{1}{T} \ - \ \frac{1}{T_{ref}}) ) \ + \ k_{cat} \ \cdot \ c_{cat} \ \cdot \ exp(-\lambda \ \cdot \ t) \ \cdot \ exp( - \frac{E_{cat}}{R} \ \cdot \ (\ \frac{1}{T} \ - \ \frac{1}{T_{ref}}) )$

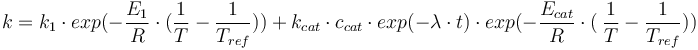
Total mass:

$m_{tot} = n_1 \ \cdot \ M_1 \ + \ n_2 \ \cdot \ M_2 \ + \ n_3 \ \cdot \ M_3 \ + \ n_4 \ \cdot \ M_4$

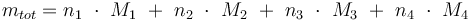
Temperature in Kelvin:

$T = \vartheta + 273$

State variables

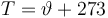
Name	Symbol	Initial value (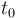$t_0$)
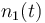
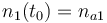
Molar number 1	$n_1(t)$	$n_1(t_0) = n_{a1}$
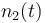
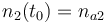
Molar number 2	$n_2(t)$	$n_2(t_0) = n_{a2}$
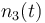
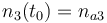
Molar number 3	$n_3(t)$	$n_3(t_0) = n_{a3}$

Parameters

Name	Symbol	Value
Steric factor	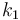$k_1$	X
Steric factor	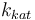$k_{kat}$	X
Activation energie	$E_1$	X
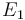
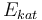
Activation energie	$E_{kat}$	X
Catalyst deactivation coefficient	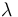$\lambda$	X

Control variables

Name	Symbol	Interval
Initial molar number 1	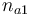$n_{a1}$	[0.4,9.0]
Initial molar number 2	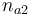$n_{a2}$	[0.4,9.0]
Initial molar number 3	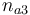$n_{a3}$	[0.4,9.0]
Concentration of the catalyst	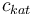$c_{kat}$	[0.0,6.0]
Initial molar number 1	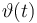$\vartheta(t)$	[20.0,100.0]