Difference between revisions of "D'Onofrio model (binary variant)"

From mintOC
Jump to: navigation, search
(→‎Reference Solutions)
 
(3 intermediate revisions by the same user not shown)
Line 32: Line 32:
 
The parameters and scenarios are as in [[D'Onofrio_chemotherapy_model]], the new fixed parameters are
 
The parameters and scenarios are as in [[D'Onofrio_chemotherapy_model]], the new fixed parameters are
  
−
<math>(c_{0,1},c_{0,2},c_{0,3},c_{0,4})=(u_0^{max},u_0^{max},0,0) \\
+
<math>(c_{0,1},c_{0,2},c_{0,3},c_{0,4})=(u_0^{max},u_0^{max},0,0), \qquad
−
(c_{1,1},c_{1,2},c_{1,3},c_{1,4})=(0,u_0^{max},u_0^{max},0).
+
(c_{1,1},c_{1,2},c_{1,3},c_{1,4})=(0,u_1^{max},u_1^{max},0).
 
</math>
 
</math>
  
 
== Reference Solutions ==
 
== Reference Solutions ==
  
−
If the problem is relaxed, i.e., we demand that <math>w(t)</math> be in the continuous interval <math>[0, 1]</math> instead of the binary choice <math>\{0,1\}</math>, the optimal solution can be determined by means of direct optimal control.  
+
If the problem is relaxed, i.e., we demand that <math>w(t)</math> be in the continuous interval <math>[0, 1]</math> instead of the binary choice <math>\{0,1\}</math>, the optimal solution can be determined by using a direct method such as collocation or Bock's direct multiple shooting method.  
  
−
The optimal objective value of the relaxed problem with  <math> n_t=6000, \, n_u=60  </math> is <math>1.30167235</math>. The objective value of the binary controls obtained by Combinatorial Integral Approimation (CIA) is <math>1.30273681</math>. 
 
  
−
<gallery caption="Reference solution plots" widths="180px" heights="140px" perrow="2">
+
The optimal objective value of scenario 2  of the relaxed problem with  <math> n_t=6000, \, n_u=100  </math> is <math>19.3561387</math>. The objective value of the binary controls obtained by Combinatorial Integral Approimation (CIA) is <math>169.45773</math>. The binary control solution was evaluated in the MIOCP by using a Merit function with additional Mayer term
−
  Image:VanderpolRelaxed 6000 100 1.pdf| Optimal relaxed controls and states determined by an direct approach with ampl_mintoc (Radau collocation) and <math>n_t=6000, \, n_u=60</math>.
+
<math> 100 \max\limits_{t\in[0,1]}\{0,x_2(t)-x_2^{max}\}+1000 \max\limits_{t\in[0,1]}\{0,x_3(t)-x_3^{max}\}  </math>.
−
Image:VanderpolCIA_6000_100_1.pdf| Optimal binary controls and states determined by an direct approach (Radau collocation) with ampl_mintoc and <math>n_t=6000, \, n_u=60</math>. The relaxed controls were approximated by Combinatorial Integral Approximation.
+
−
</gallery>
+
  
  
 +
<gallery caption="Reference solution plots" widths="180px" heights="140px" perrow="2">
 +
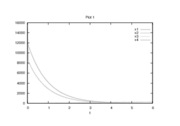
Image:DonofrioRelaxed 6000 60 1.png| Optimal relaxed differential states determined by an direct approach with ampl_mintoc (Radau collocation)  and <math>n_t=6000, \, n_u=100</math>.
 +
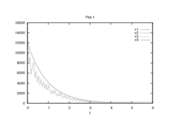
Image:DonofrioCIA 6000 60 1.png| Optimal binary differential states determined by an direct approach (Radau collocation) with ampl_mintoc and <math>n_t=6000, \, n_u=100</math>. The relaxed controls were approximated by Combinatorial Integral Approximation.
 +
</gallery>
  
 
== Source Code ==
 
== Source Code ==
  
 
Model description is available in
 
Model description is available in
−
* [[:Category:AMPL | AMPL code]] at [[Van der Pol Oscillator binary variant(AMPL)]]
+
* [[:Category:AMPL | AMPL code]] at [[D'Onofrio model, binary variant (AMPL)]]
  
  

Latest revision as of 17:33, 11 January 2018

D'Onofrio model (binary variant)
State dimension: 1
Differential states: 4
Discrete control functions: 4
Path constraints: 2

This site describes a D'Onofrio model variant with four binary controls instead which of only two continuous controls. The continuous controls are replaced via the outer convexifacation method.

Mathematical formulation

For t \in [t_0, t_f] the optimal control problem is given by

\begin{array}{llcl} \displaystyle \min_{x, u} & x_0(t_f) &+& \alpha \int_{t_0}^{t_f} u_0(t)^2 \text{d}t \\[1.5ex] \mbox{s.t.} & \dot{x}_0 & = & - \zeta x_0 \text{ln} \left( \frac{x_0}{x_1} \right) - \sum\limits_{i=1}^{4} w_i\;c_{1,i}\; F \; x_0 , \\ & \dot{x}_1 & = & b x_0 - \mu x_1 - d x_0^{\frac{2}{3}}x_1 -\sum\limits_{i=1}^{4} w_i c_{0,i} \; G x_1 - \sum\limits_{i=1}^{4} w_i\;c_{1,i} \; \eta x_1, \\ & \dot{x}_2 & = & \sum\limits_{i=1}^{4} w_i\;c_{0,i}, \\ & \dot{x}_3 & = & \sum\limits_{i=1}^{4} w_i\;c_{1,i}, \\ [1.5ex] & x_2 & \leq & x_2^{max}, \\ & x_3 & \leq & x_3^{max},\\ & 1 &=& \sum\limits_{i=1}^{4}w_i(t), \\ & w_i(t) &\in& \{0, 1\}, \quad i=1\ldots 4. \end{array}


Parameters

The parameters and scenarios are as in D'Onofrio_chemotherapy_model, the new fixed parameters are

(c_{0,1},c_{0,2},c_{0,3},c_{0,4})=(u_0^{max},u_0^{max},0,0), \qquad (c_{1,1},c_{1,2},c_{1,3},c_{1,4})=(0,u_1^{max},u_1^{max},0).

Reference Solutions

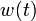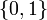If the problem is relaxed, i.e., we demand that w(t) be in the continuous interval [0, 1] instead of the binary choice \{0,1\}, the optimal solution can be determined by using a direct method such as collocation or Bock's direct multiple shooting method.


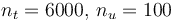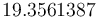The optimal objective value of scenario 2 of the relaxed problem with n_t=6000, \, n_u=100 is 19.3561387. The objective value of the binary controls obtained by Combinatorial Integral Approimation (CIA) is 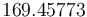169.45773. The binary control solution was evaluated in the MIOCP by using a Merit function with additional Mayer term 100 \max\limits_{t\in[0,1]}\{0,x_2(t)-x_2^{max}\}+1000 \max\limits_{t\in[0,1]}\{0,x_3(t)-x_3^{max}\} .


  • Reference solution plots

  • Optimal relaxed differential states determined by an direct approach with ampl_mintoc (Radau collocation) and n_t=6000, \, n_u=100.

  • Optimal binary differential states determined by an direct approach (Radau collocation) with ampl_mintoc and n_t=6000, \, n_u=100. The relaxed controls were approximated by Combinatorial Integral Approximation.

Source Code

Model description is available in

Retrieved from "https://mintoc.de/index.php?title=D%27Onofrio_model_(binary_variant)&oldid=2233"