Difference between revisions of "Double Tank multimode problem"

From mintOC
Jump to: navigation, search
(Created page with "{{Dimensions |nd = 1 |nx = 3 |nw = 3 |nre = 2 }}<!-- Do not insert line break here or Dimensions Box moves up in the layout... -->This site describ...")
 
 
(3 intermediate revisions by the same user not shown)
Line 1: Line 1:
 
{{Dimensions
 
{{Dimensions
 
|nd        = 1
 
|nd        = 1
−
|nx        = 3
+
|nx        = 2
 
|nw        = 3
 
|nw        = 3
 
|nre      = 2
 
|nre      = 2
Line 23: Line 23:
 
</math>
 
</math>
  
−
 
−
Here the differential states <math>(x_0, x_1)</math> describe the biomasses of prey and predator, respectively. The third differential state is used here to transform the objective, an integrated deviation, into the Mayer formulation <math>\min \; x_2(t_f)</math>. This problem variant allows to choose between three different fishing options.
 
  
 
== Parameters ==
 
== Parameters ==
Line 30: Line 28:
 
These fixed values are used within the model.
 
These fixed values are used within the model.
  
−
<math>
+
<math> T=10, c_1=1, c_2=0.5, c_3=2, k_1=2, k_2=3. </math>
−
\begin{array}{rcl}
+
−
[t_0, t_f] &=& [0, 12],\\
+
−
(c_{0,1}, c_{1,1}) &=& (0.2, 0.1),\\
+
−
(c_{0,2}, c_{1,2}) &=& (0.4, 0.2),\\
+
−
(c_{0,3}, c_{1,3}) &=& (0.01, 0.1).
+
−
\end{array}
+
−
</math>
+
  
 
== Reference Solutions ==
 
== Reference Solutions ==
Line 43: Line 34:
 
If the problem is relaxed, i.e., we demand that <math>w(t)</math> be in the continuous interval <math>[0, 1]</math> instead of the binary choice <math>\{0,1\}</math>, the optimal solution can be determined by means of direct optimal control.  
 
If the problem is relaxed, i.e., we demand that <math>w(t)</math> be in the continuous interval <math>[0, 1]</math> instead of the binary choice <math>\{0,1\}</math>, the optimal solution can be determined by means of direct optimal control.  
  
−
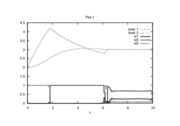
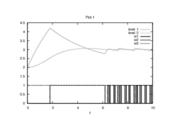
The optimal objective value of the relaxed problem with  <math> n_t=12000, \, n_u=400 </math> is <math>x_2(t_f) =1.82875272</math>. The objective value of the binary controls obtained by Combinatorial Integral Approimation (CIA) is <math>x_2(t_f) =1.82878681</math>.   
+
The optimal objective value of the relaxed problem with  <math> n_t=12000, \, n_u=100 </math> is <math>2.59106823</math>. The objective value of the binary controls obtained by Combinatorial Integral Approimation (CIA) is <math>2.59121008</math>.   
  
 
<gallery caption="Reference solution plots" widths="180px" heights="140px" perrow="2">
 
<gallery caption="Reference solution plots" widths="180px" heights="140px" perrow="2">
−
  Image:MmlotkaRelaxed_12000_30_1.png| Optimal relaxed controls and states determined by an direct approach with ampl_mintoc (Radau collocation)  and <math>n_t=12000, \, n_u=400</math>.
+
  Image:MmdoubletankRelaxed 12000 120 1.png| Optimal relaxed controls and states determined by an direct approach with ampl_mintoc (Radau collocation)  and <math>n_t=12000, \, n_u=100</math>.
−
  Image:MmlotkaCIA 12000 30 1.png| Optimal binary controls and states determined by an direct approach (Radau collocation) with ampl_mintoc and <math>n_t=12000, \, n_u=400</math>. The relaxed controls were approximated by Combinatorial Integral Approximation.
+
  Image:MmdoubletankCIA_12000_120_1.png| Optimal binary controls and states determined by an direct approach (Radau collocation) with ampl_mintoc and <math>n_t=12000, \, n_u=100</math>. The relaxed controls were approximated by Combinatorial Integral Approximation.
 
</gallery>
 
</gallery>
  
  
 +
== Source Code ==
  
 +
Model description is available in
 +
* [[:Category:AMPL | AMPL code]] at [[Double Tank multimode problem (AMPL)]]
  
  
Line 63: Line 57:
 
[[Category:Chattering]]
 
[[Category:Chattering]]
 
[[Category:Sensitivity-seeking arcs]]
 
[[Category:Sensitivity-seeking arcs]]
−
[[Category:Population dynamics]]
+
 
  
  

Latest revision as of 09:37, 14 March 2020

Double Tank multimode problem
State dimension: 1
Differential states: 2
Discrete control functions: 3
Interior point equalities: 2

This site describes a Double tank problem variant with three binary controls instead of only one control.

Mathematical formulation

The mixed-integer optimal control problem is given by

\begin{array}{llll} \displaystyle \min_{x,w} & \displaystyle \int_{0}^{T} & k_1(x_2-k_2)^2 \; \text{d}t\\[1.5ex] \mbox{s.t.} & \dot{x}_1 & = \sum\limits_{i=1}^{3} c_{i}\; w_i,-\sqrt{x_1}, \\[1.5ex] & \dot{x}_2 & = \sqrt{x_1}-\sqrt{x_2}, \\[1.5ex] & x(0) & = (2,2)^T, \\[1.5ex] & 1 & = \sum\limits_{i=1}^{3}w_i(t), \\ & w_i(t) &\in \{0, 1\}, \quad i=1\ldots 3. \end{array}


Parameters

These fixed values are used within the model.

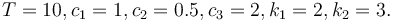
T=10, c_1=1, c_2=0.5, c_3=2, k_1=2, k_2=3.

Reference Solutions

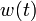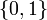If the problem is relaxed, i.e., we demand that w(t) be in the continuous interval [0, 1] instead of the binary choice \{0,1\}, the optimal solution can be determined by means of direct optimal control.

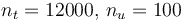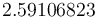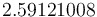The optimal objective value of the relaxed problem with n_t=12000, \, n_u=100 is 2.59106823. The objective value of the binary controls obtained by Combinatorial Integral Approimation (CIA) is 2.59121008.

  • Reference solution plots

  • Optimal relaxed controls and states determined by an direct approach with ampl_mintoc (Radau collocation) and n_t=12000, \, n_u=100.

  • Optimal binary controls and states determined by an direct approach (Radau collocation) with ampl_mintoc and n_t=12000, \, n_u=100. The relaxed controls were approximated by Combinatorial Integral Approximation.


Source Code

Model description is available in

Retrieved from "https://mintoc.de/index.php?title=Double_Tank_multimode_problem&oldid=2327"