Lotka Volterra (terminal constraint violation)
| Lotka Volterra (terminal constraint violation) | |
|---|---|
| State dimension: | 1 |
| Differential states: | 2 |
| Discrete control functions: | 1 |
| Interior point inequalities: | 1 |
| Interior point equalities: | 2 |
This site describes a Lotka Volterra variant where a terminal inequality constraint on the differential states is added. A violation of this constraint is penalized as part of the Mayer objective.
Mathematical formulation
The mixed-integer optimal control problem is given by
![\begin{array}{llclr}
\displaystyle \min_{x, w, s} & x_2(t_f) + 10s \\[1.5ex]
\mbox{s.t.}
& \dot{x}_0 & = & x_0 - x_0 x_1 - \; c_0 x_0 \; w, \\
& \dot{x}_1 & = & - x_1 + x_0 x_1 - \; c_1 x_1 \; w, \\
& \dot{x}_2 & = & (x_0 - 1)^2 + (x_1 - 1)^2, \\[1.5ex]
& x_0 & \geq & 1.1 - s, \\
& x(0) &=& (0.5, 0.7, 0)^T, \\
& w(t) &\in& \{0, 1\}, \\
& s & \geq & 0.
\end{array}](https://mintoc.de/images/math/6/6/5/665c248e3d1423f75fd785c6d45adc24.png)
Here the differential states 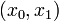 describe the biomasses of prey and predator, respectively. The third differential state is used here to transform the objective, an integrated deviation, into the Mayer formulation
describe the biomasses of prey and predator, respectively. The third differential state is used here to transform the objective, an integrated deviation, into the Mayer formulation 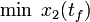 . This problem variant penalizes a biomass x(0) that is below 1.1 at the end of the time horizon.
. This problem variant penalizes a biomass x(0) that is below 1.1 at the end of the time horizon.
Parameters
These fixed values are used within the model.
![\begin{array}{rcl}
[t_0, t_f] &=& [0, 12],\\
(c_{0}, c_{1}) &=& (0.4, 0.2),
\end{array}](https://mintoc.de/images/math/7/8/5/78569f6bce72b25f348e1511303041a0.png)
Reference Solutions
If the problem is relaxed, i.e., we demand that  is in the continuous interval
is in the continuous interval ![[0, 1]](https://mintoc.de/images/math/c/c/f/ccfcd347d0bf65dc77afe01a3306a96b.png) rather than being binary, the optimal solution can be determined by means of direct optimal control.
rather than being binary, the optimal solution can be determined by means of direct optimal control.
The optimal objective value of the relaxed problem with  is
is 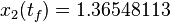 . The objective value of the solution with binary controls obtained by Combinatorial Integral Approximation (CIA) is
. The objective value of the solution with binary controls obtained by Combinatorial Integral Approximation (CIA) is 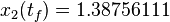 .
.
- Reference solution plots