Truck cruise control
| Truck cruise control | |
|---|---|
| State dimension: | 1 |
| Differential states: | 3 |
| Discrete control functions: | 1 |
| Interior point equalities: | 6 |
The truck cruise control problem uses a quite simple truck model. It realizes several objective criteria as fuel consumption, traveling time and driver comfort are competing against each other. The problem is formulated in terms of the traveled distance.
Mathematical formulation (under construction)
For ![s \in [0, s_f]](https://mintoc.de/images/math/0/1/8/0184070f97679227d901aeacecb7ba60.png) almost everywhere the mixed-integer optimal control problem is given by
almost everywhere the mixed-integer optimal control problem is given by
![\begin{alignat}{2}
& \displaystyle \min_{x, u, w} && \lambda_\text{dev} \Phi_\text{dev} + \lambda_\text{fuel} \Phi_\text{fuel} + \lambda_\text{comf} \Phi_\text{comf} \\[1.5ex]
& \mbox{s.t.}
& \dot{x}_0 & = \frac{1}{m x_0} \left( M_\text{acc} - \frac{i_A}{r_\text{stat}}M_\text{brk} - M_\text{air} - M_\text{road} \right) \\
&& \dot{x}_1 & = \frac{1}{x_0} Q_\text{fuel} (neng, u_0) \\
&& \dot{x}_2 & = -4.208 \; x_0 - 0.396 \; x_2 - 0.47 \; x_0^2 - 3.564 \; x_0^3 \\
&& & \quad - 20.967 \; w + 6.265 \; x_0^2 \; w + 46 \; x_0 \; w^2 + 61.4 \; w^3 \\
&& x(0) & = (0.4655,0,0)^T, \\
&& x(T) & = (0,0,0)^T, \\
&& w(t) & \in \{-0.05236,0.05236\}.
\end{alignat}](https://mintoc.de/images/math/6/7/f/67fd7d4a608f48ba78098b79e5c172ea.png)
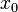 is the velocity of the truck in m/s,
is the velocity of the truck in m/s, 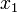 is the fuel consumption in liters, the control function
is the fuel consumption in liters, the control function 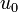 is the induced engine torque in Nm,
is the induced engine torque in Nm, 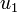 is the combined engine brake torque. This model goes back to Garrard[Garrard1977]Author: Garrard, W.L.; Jordan, J.M.
is the combined engine brake torque. This model goes back to Garrard[Garrard1977]Author: Garrard, W.L.; Jordan, J.M.
Journal: Automatica
Pages: 497--505
Title: Design of Nonlinear Automatic Control Systems
Volume: 13
Year: 1977 .
.
The equality constraints 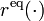 will often fix the initial values, i.e.,
will often fix the initial values, i.e., 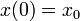 , or impose a periodicity constraint.
, or impose a periodicity constraint.
Extensions (under construction)
- For some problems the functions may as well depend explicitely on the time
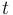 .
. - The differential equations might depend on state-dependent switches.
- The variables may include boolean variables.
- The underlying process might be a multistage process.
- The dynamics might be unstable.
- There might be an underlying network topology.
- The integer control functions might have been (re)formulated by means of an outer convexification.
Note that a Lagrange term 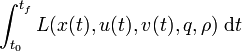 can be transformed into a Mayer-type objective functional.
can be transformed into a Mayer-type objective functional.