Difference between revisions of "Urethane"
RobertLampel (Talk | contribs) (→Chemical background) |
RobertLampel (Talk | contribs) (→Chemical background) |
||
| Line 24: | Line 24: | ||
<tr style="border-bottom: 2pt solid black"> | <tr style="border-bottom: 2pt solid black"> | ||
<th style="border-right:2pt solid black; padding:2pt">Letter</th> | <th style="border-right:2pt solid black; padding:2pt">Letter</th> | ||
| − | <th>Substance</th> | + | <th style="padding:2pt">Substance</th> |
</tr> | </tr> | ||
<tr> | <tr> | ||
Revision as of 11:02, 13 November 2024
| Urethane | |
|---|---|
| State dimension: | 1 |
| Differential states: | 11 |
| Discrete control functions: | 2 |
| Path constraints: | 4 |
| Interior point equalities: | 11 |
This page describes the Optimal Experimental Design Problem for the Urethane Reaction. The following formulation is taken from [1] and [2].
Contents
[hide]Chemical background
The reaction scheme of the urethane reaction is as follows:
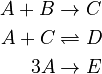
For ease of notation the chemical substances use the abbreviations
| Letter | Substance |
|---|---|
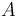 |
Phenyl Isocyanate |
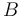 |
Butanol |
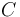 |
Urethane (Main Product) |
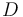 |
Allophanate (Secondary Product) |
 |
Isocyanurate (Byproduct) |
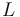 |
Dimethyl Sulfoxide |
The reactor for the urethane reaction is a stirred tank and can be operated as a batch or semi-batch process with up to two feeds. In the reactor, phenyl isocyanate and butanol can be initially charged in the solvent dimethyl sulfoxide. In feed 1, phenyl isocyanate in dimethyl sulfoxide can be added, and in feed 2, butanol in dimethyl sulfoxide can be added. The internal temperature of the reactor is controllable.
Mathematical formulation
We can describe this process using a nonlinear DAE model
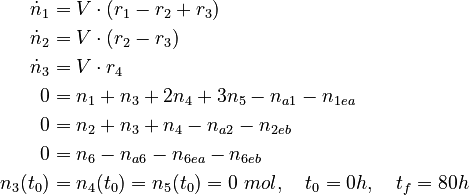
with
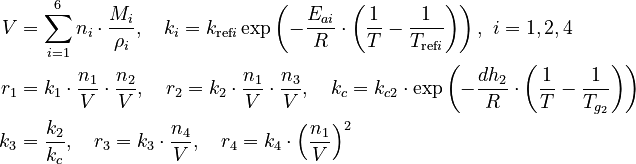
The molar numbers 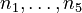 of the species
of the species 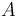 to
to  and
and 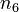 of the solvent
of the solvent 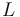 are the state variables of the DAE system.
There are eight unknown parameters in this model:
are the state variables of the DAE system.
There are eight unknown parameters in this model:
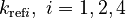
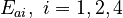
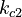 (for the reference temperature
(for the reference temperature  )
) of the reversible reaction
of the reversible reactionThe two feeds are modelled by two monotonously increasing control functions
![\text{feed}_a,\text{feed}_b: \ [t_0,t_f] \rightarrow [0,1]](https://mintoc.de/images/math/1/b/8/1b8534800634691944bd17daec1b10bf.png)
describing the profiles of the accumulated feeds. Multiplied with the initial molar numbers within the feed vessels, we get the feed molar numbers:
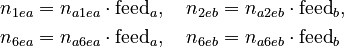
The third control function is the temperature profile
![T: [t_0,t_f] \rightarrow [293.16 \ K, \ 473.16 \ K]](https://mintoc.de/images/math/9/5/3/9530558cca3d00bba6ea5d58b4b64609.png)
Each experiment lasts 80 hours. The beginning is Monday, 8 pm, the end Thursday, 4 pm. During the nights, the feed rates and the heating=cooling rate have to be zero due to safety rules. Further control variables for experimental design are
![MV_1 \in [0.1, 10], \ MV_2 \in [0, 1000]](https://mintoc.de/images/math/8/4/d/84d642bb2a5fa4d97c403d9a670b6c98.png) , and
, and ![MV_3 \in [0, 10]](https://mintoc.de/images/math/9/7/3/9730e32c3f23a9e86d44efc2510f4ed3.png)
![g_a \in [0, 0.8], \ g_{aea} \in [0, 0.9]](https://mintoc.de/images/math/b/7/a/b7aa0673ebf94e13850a6dcebde5c7b4.png) , and
, and ![g_{aeb} \in [0, 1]](https://mintoc.de/images/math/c/f/0/cf0bfa5a3b64a479b73da111ce671caa.png)
![V_a \in [0 m^3 , 0.00075 m^3 ]](https://mintoc.de/images/math/f/f/1/ff1e79de3f4ebe9005c130872eb7544c.png) of the species in the reactor.
of the species in the reactor.These quantities are connected to the initial molar numbers as follows
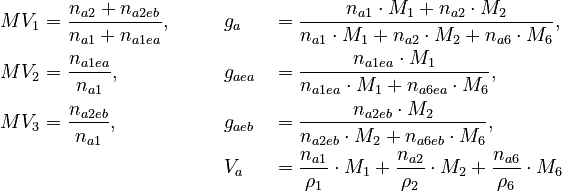
The remaining quantities are constants and shown in the parameter section. Three measurement methods are available:
In each experiment, 16 measurements can be selected out of 30 possible ones. We parametrize the time depending control functions using piecewise linear and continuous polynomials. Altogether we have 90 experimental design variables for each experiment: 7 control variables, 7 initial molar numbers, 30 weights on the measurements, and 46 variables due to the parametrization of the control functions.
Parameters
| Intial Values | |
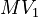 |
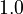 |
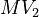 |
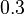 |
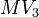 |
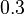 |
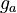 |
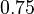 |
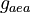 |
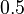 |
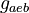 |
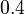 |
 |
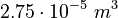 |
| Constants | ||
| Molar Mass | Density | Reference Temperature |
|---|---|---|
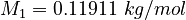 |
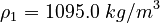 |
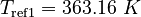 |
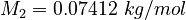 |
 |
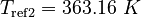 |
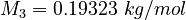 |
 |
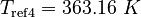 |
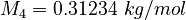 |
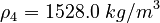 |
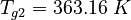 |
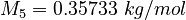 |
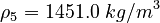 |
molar gas constant  |
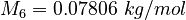 |
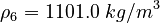 |
|
Optimal Experimental Design Problem
Now we formulate the OED problem as described in [3].
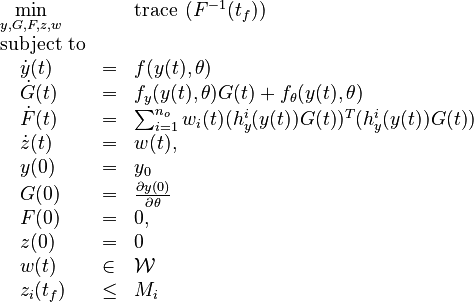
Here 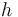 is the observed function. The
evolution of the symmetric matrix
is the observed function. The
evolution of the symmetric matrix 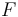 is given by the weighted sum of observability Gramians
is given by the weighted sum of observability Gramians
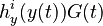 for each observed function of states. The weights
for each observed function of states. The weights 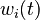 are the sampling decisions.
are the sampling decisions.
Miscellaneous and Further Reading
To be specified.
References
[1] "Numerische Methoden für Optimale Versuchsplanungsprobleme bei nichtlinearen DAE-Modellen " by S. Körkel
[2] "Numerical methods for optimum experimental design in DAE systems" by I. Bauer, H.G. Bock, S. Körkel and J.P. Schlöder
[3] "Optimal Experimental Design for Universal Differential Equations" by C. Plate, C.J. Martensen and S. Sager