Category:Problem characterization

From mintOC
Jump to: navigation, search

This is a super-category of all problem description categories, i.e., it lists all subcategories that have been defined so far. Note that the category Category:MIOCP contains a list of all mixed-integer optimal control problems in the library. The following graph shows the (yet incomplete) organization of categories on mintoc.de. {{#categorytree: Problem characterization|depth=5|mode=pages|showcount}}

The MIOCPs in our benchmark library have different characteristics. Beside its origins from application fields such as mechanical engineering, aeronautics, transport, systems biology, chemical engineering and the like, we propose three levels to characterize a control problem. First, characteristics of the model from a mathematical point of view, second the formulation of the optimization problem, and third characteristics of an optimal solution from a control theory point of view. Additionally, there are flags concerning the application are and the format the problems are specified in.

Although we strive for a standardized problem formulation, we do not formulate a specific generic formulation as such. Such a formulation is not even agreed upon for PDEs, let alone the possible extensions in the direction of algebraic variables, network topologies, logical connections, multi-stage processes, MPEC constraints, multiple objectives, functions including higher-order derivatives and much more that might come in. Therefore we chose to start with a very abstract formulation, formulate every control problem in its specific way as is adequate and to connect the two by using a characterization.

On the most abstract level, we want to solve an optimization problem that can be written as

\begin{array}{lrcl} \displaystyle \min_{x, u, v} & \Phi[x,u,v]) \\[1.5ex] \mbox{s.t.} & 0 & = & F[x,u,v], \\ & 0 & \le & C[x,u,v], \\ & 0 & = & \Gamma[x]. \end{array}

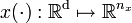Here x(\cdot): \R^\mathrm{d} \mapsto \R^{n_x} denotes the differential-algebraic states in a 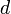d-dimensional space. Note that we use the notation common in control theory with 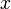x as differential states and 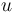u as controls, not the PDE formulation with 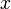x as independent variable and 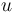u as differential states. Until now, for most applications we have 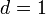d=1 and the independent variable time t \in [t_0, t_f], the case of ordinary or algebraic differential equations. 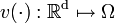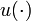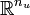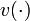u(\cdot): \R^\mathrm{d} \mapsto \R^{n_u} and v(\cdot): \R^\mathrm{d} \mapsto \Omega are controls, where u(\cdot) are continuous values that map to \R^{n_u}, and v(\cdot) are controls that map to a finite set 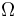\Omega. We allow also constant-in-time or constant-in-space control values rather than distributed controls.

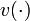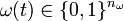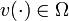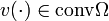We will also use the term integer control for v(\cdot), while binary control refers to \omega(t) \in \{0,1\}^{n_{\omega}} that will be introduced later. We use the expression relaxed, whenever a restriction v(\cdot) \in \Omega is relaxed to a convex control set, which is typically the convex hull, v(\cdot) \in \mathrm{conv} \Omega.

Basically two different kinds of switching events are at the origin of hybrid systems, controllable and state-dependent ones. The first kind is due to degrees of freedom for the optimization, in particular with controls that may only take values from a finite set. The second kind is due to state-dependent switches in the model equations, e.g., ground contact of a robot leg or overflow of weirs in a distillation column. The focus in the benchmark library is on the first kind of switches, whereas the second one is of course important for a classification of the model equations, as for certain MIOCPs both kinds occur.

The model equations are described by the functional F[\cdot] (model characterization). The objective functional \Phi[\cdot], the constraints C[\cdot] that may include control- and path-constraints, and the interior point constraints \Gamma[x] that specify also the boundary conditions are classified as objective characterization objective characterization. Characteristics of an optimal solution from a control theory point of view are listed as solution characterization.

The formulation of optimization problems is typically not unique. Sometimes, as in the case of MPEC reformulations of state-dependent switches [Baumrucker2009]Author: B.T. Baumrucker; L.T. Biegler
Journal: Journal of Process Control
Note: Special Section on Hybrid Systems: Modeling, Simulation and Optimization
Number: 8
Pages: 1248--1256
Title: MPEC strategies for optimization of a class of hybrid dynamic systems
Volume: 19
Year: 2009
Link to Google Scholar, disjunctive programming [Grossmann2002]Author: I.E. Grossmann
Journal: Optimization and Engineering
Pages: 227--252
Title: Review of Nonlinear Mixed-Integer and Disjunctive Programming Techniques
Volume: 3
Year: 2002
Link to Google Scholar, or outer convexification [Sager2009]Author: Sager, S.; Reinelt, G.; Bock, H.G.
Journal: Mathematical Programming
Number: 1
Pages: 109--149
Title: Direct Methods With Maximal Lower Bound for Mixed-Integer Optimal Control Problems
Url: http://mathopt.de/PUBLICATIONS/Sager2009.pdf
Volume: 118
Year: 2009
Link to Google Scholar, reformulations may be seen as part of the solution approach in the sense of the modeling for optimization paradigm [Oldenburg2008]Author: J. Oldenburg; W. Marquardt
Journal: Computers \& Chemical Engineering
Number: 10
Pages: 2346--2364
Title: Disjunctive modeling for optimal control of hybrid systems
Volume: 32
Year: 2008
Link to Google Scholar. Even in obvious cases, such as a Mayer term versus a Lagrange term formulation, they may be mathematically, but not necessarily algorithmically equivalent. We propose to use either the original or the most adequate formulation of the optimization problem and list possible reformulations as variants.


References

[Baumrucker2009]B.T. Baumrucker; L.T. Biegler (2009): MPEC strategies for optimization of a class of hybrid dynamic systems. Journal of Process Control, 19, 1248--1256Link to Google Scholar
[Grossmann2002]I.E. Grossmann (2002): Review of Nonlinear Mixed-Integer and Disjunctive Programming Techniques. Optimization and Engineering, 3, 227--252Link to Google Scholar
[Oldenburg2008]J. Oldenburg; W. Marquardt (2008): Disjunctive modeling for optimal control of hybrid systems. Computers \& Chemical Engineering, 32, 2346--2364Link to Google Scholar
[Sager2009]Sager, S.; Reinelt, G.; Bock, H.G. (2009): Direct Methods With Maximal Lower Bound for Mixed-Integer Optimal Control Problems. Mathematical Programming, 118, 109--149Link to Google Scholar

Subcategories

This category has the following 6 subcategories, out of 6 total.

A

I

M

O

S

Retrieved from "https://mintoc.de/index.php?title=Category:Problem_characterization&oldid=1387"