Category:Solution characterization

From Mintoc

The classification that we propose for switching decisions is based on insight from Pontryagin's maximum principle ^[1] applied here only to the relaxation of the binary control functions 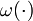, denoted by . In the analysis of linear control problems one distinguishes three cases: bang-bang arcs, sensitivity-seeking arcs, and path-constrained arcs, ^[2], where an arc is defined to be a nonzero time-interval. Of course a problem's solution can show two or even all three behaviors at once on different time arcs.

Additionally we characterize solutions, whenever chattering or sliding mode behavior occurs.

References

1. ↑ Pontryagin, L. S., Boltyanski, V. G., Gamkrelidze, R. V., & Miscenko, E. F. (1962). The Mathematical Theory of Optimal Processes. Chichester: Wiley. ^Bib
2. ↑ Srinivasan, B., Palanki, S., & Bonvin, D. (2003). Dynamic Optimization of Batch Processes: I. Characterization of the Nominal Solution. Computers and Chemical Engineering, 27, 1. ^Bib