Difference between revisions of "Fuller's problem"
(→Source Code) |
(→Source Code) |
||
| Line 43: | Line 43: | ||
== Source Code == | == Source Code == | ||
| − | + | * [[:Category:optimica | optimica]] at [[Fuller's Problem (optimica)]] | |
| − | + | ||
=== C Code === | === C Code === | ||
Revision as of 11:03, 7 August 2009
| Fuller's problem | |
|---|---|
| State dimension: | 1 |
| Differential states: | 2 |
| Discrete control functions: | 1 |
| Interior point equalities: | 4 |
The first control problem with an optimal chattering solution was given by <bibref>Fuller1963</bibref>. An optimal trajectory does exist for all initial and terminal values in a vicinity of the origin. As Fuller showed, this optimal trajectory contains a bang-bang control function that switches infinitely often.
The mathematical equations form a small-scale ODE model. The interior point equality conditions fix initial and terminal values of the differential states.
Contents
[hide]Mathematical formulation
For ![t \in [t_0, t_f]](https://mintoc.de/images/math/5/5/8/55823791d9100bcb5461801aff4f6edd.png) almost everywhere the mixed-integer optimal control problem is given by
almost everywhere the mixed-integer optimal control problem is given by
![\begin{array}{llcl}
\displaystyle \min_{x, w} & \int_{0}^{1} x_0^2 \; \mathrm{d} t \\[1.5ex]
\mbox{s.t.} & \dot{x}_0(t) & = & x_1(t), \\
& \dot{x}_1(t) & = & 1 - 2 \; w(t), \\[1.5ex]
& x(0) &=& x_S, \\
& x(t_f) &=& x_T, \\
& w(t) &\in& \{0, 1\}.
\end{array}](https://mintoc.de/images/math/b/c/8/bc817f0912abd1c57882137cc7ea7a5d.png)
Parameters
We use 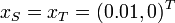 .
.
Reference Solutions
Source Code
C Code
The differential equations in C code:
Miscellaneous and further reading
An extensive analytical investigation of this problem and a discussion of the ubiquity of Fuller's problem can be found in <bibref>Zelikin1994</bibref>, a recent investigation of chattering controls in relay feedback systems in <bibref>Johansson2002</bibref>.
References
<bibreferences/>