Difference between revisions of "Fuller's problem"
(→Source Code) |
m |
||
| Line 14: | Line 14: | ||
For <math>t \in [t_0, t_f]</math> almost everywhere the mixed-integer optimal control problem is given by | For <math>t \in [t_0, t_f]</math> almost everywhere the mixed-integer optimal control problem is given by | ||
| + | <p> | ||
<math> | <math> | ||
\begin{array}{llcl} | \begin{array}{llcl} | ||
| Line 24: | Line 25: | ||
\end{array} | \end{array} | ||
</math> | </math> | ||
| + | </p> | ||
== Parameters == | == Parameters == | ||
| Line 50: | Line 52: | ||
== Source Code == | == Source Code == | ||
| + | * [[:Category:C | C code]] at [[Fuller's Problem (C)]] | ||
* [[:Category:optimica | optimica]] at [[Fuller's Problem (optimica)]] | * [[:Category:optimica | optimica]] at [[Fuller's Problem (optimica)]] | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
== Miscellaneous and further reading == | == Miscellaneous and further reading == | ||
Revision as of 16:29, 11 August 2009
| Fuller's problem | |
|---|---|
| State dimension: | 1 |
| Differential states: | 2 |
| Discrete control functions: | 1 |
| Interior point equalities: | 4 |
The first control problem with an optimal chattering solution was given by <bibref>Fuller1963</bibref>. An optimal trajectory does exist for all initial and terminal values in a vicinity of the origin. As Fuller showed, this optimal trajectory contains a bang-bang control function that switches infinitely often.
The mathematical equations form a small-scale ODE model. The interior point equality conditions fix initial and terminal values of the differential states.
Contents
Mathematical formulation
For ![t \in [t_0, t_f]](https://mintoc.de/images/math/5/5/8/55823791d9100bcb5461801aff4f6edd.png)
almost everywhere the mixed-integer optimal control problem is given by
![\begin{array}{llcl}
\displaystyle \min_{x, w} & \int_{0}^{1} x_0^2 \; \mathrm{d} t \\[1.5ex]
\mbox{s.t.} & \dot{x}_0(t) & = & x_1(t), \\
& \dot{x}_1(t) & = & 1 - 2 \; w(t), \\[1.5ex]
& x(0) &=& x_S, \\
& x(t_f) &=& x_T, \\
& w(t) &\in& \{0, 1\}.
\end{array}](https://mintoc.de/images/math/b/c/8/bc817f0912abd1c57882137cc7ea7a5d.png)
Parameters
We use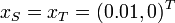 
.
Reference Solutions
Solutions obtained with optimica
The solution found for the relaxed Fuller's problem with optimica using the solver Ipopt (with the linear solver MA27) is obtained with 12 iterations and the objective is 1.5296058259296967e-05.
Source Code
Miscellaneous and further reading
An extensive analytical investigation of this problem and a discussion of the ubiquity of Fuller's problem can be found in <bibref>Zelikin1994</bibref>, a recent investigation of chattering controls in relay feedback systems in <bibref>Johansson2002</bibref>.
References
<bibreferences/>
