Difference between revisions of "Diels-Alder Reaction Experimental Design"
From mintOC
(→Model Formulation) |
(→Model Formulation) |
||
| Line 37: | Line 37: | ||
<p> | <p> | ||
<math> | <math> | ||
| − | \begin{array}{ | + | \begin{array}{cll} |
| − | \displaystyle \min_{x, G, F, u} & trace(F^{-1} (t_{t_f})) \\[1.5ex] | + | \displaystyle \min_{x, G, F, u} && trace(F^{-1} (t_{t_f})) \\[1.5ex] |
| − | \mbox{s.t.} \dot{n_1}(t) & = -k \cdot \frac{n_1(t) \ \cdot \ n_2(t)}{m_{tot}}, \\ | + | \mbox{s.t.} \\ |
| − | \dot{n_2}(t) & = -k \cdot \frac{n_1(t) \ \cdot \ n_2(t)}{m_{tot}}, \\ | + | \dot{n_1}(t) & = & -k \cdot \frac{n_1(t) \ \cdot \ n_2(t)}{m_{tot}}, \\ |
| − | \dot{n_2}(t) & = \ \ k \cdot \frac{n_1(t) \ \cdot \ n_2(t)}{m_{tot}}, \\ | + | \dot{n_2}(t) & = & -k \cdot \frac{n_1(t) \ \cdot \ n_2(t)}{m_{tot}}, \\ |
| − | 0 & = g(x(t_o),x(t_f),p) \\ | + | \dot{n_2}(t) & = & \ \ k \cdot \frac{n_1(t) \ \cdot \ n_2(t)}{m_{tot}}, \\ |
| − | 0 & \ge c(x,u,p), \forall \, t \in I\\ | + | 0 & = & g(x(t_o),x(t_f),p) \\ |
| − | 0 & = | + | 0 & \ge & c(x,u,p), \forall \, t \in I\\ |
| − | x & \in \mathcal{X},\,u \in \mathcal{U},\, p \in P. | + | 0 & = & h(x,u,p), \forall \, t \in I \\ |
| + | x & \in & \mathcal{X},\,u \in \mathcal{U},\, p \in P. | ||
\end{array} | \end{array} | ||
</math> | </math> | ||
Revision as of 11:31, 4 December 2015
This page can now be filled with content.
Model Formulation
Differential equation system:
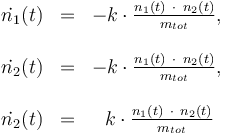
Reaction velocity constant:
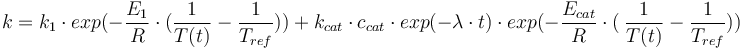
Total mass:
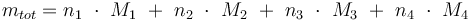
Temperature in Kelvin:
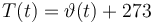
![\begin{array}{cll}
\displaystyle \min_{x, G, F, u} && trace(F^{-1} (t_{t_f})) \\[1.5ex]
\mbox{s.t.} \\
\dot{n_1}(t) & = & -k \cdot \frac{n_1(t) \ \cdot \ n_2(t)}{m_{tot}}, \\
\dot{n_2}(t) & = & -k \cdot \frac{n_1(t) \ \cdot \ n_2(t)}{m_{tot}}, \\
\dot{n_2}(t) & = & \ \ k \cdot \frac{n_1(t) \ \cdot \ n_2(t)}{m_{tot}}, \\
0 & = & g(x(t_o),x(t_f),p) \\
0 & \ge & c(x,u,p), \forall \, t \in I\\
0 & = & h(x,u,p), \forall \, t \in I \\
x & \in & \mathcal{X},\,u \in \mathcal{U},\, p \in P.
\end{array}](https://mintoc.de/images/math/5/8/f/58f1d83c9d7a1cad6e7da728f717534f.png)
| Name | Symbol | Initial value (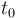 ) )
|
| Molar number 1 | 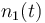
|
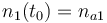
|
| Molar number 2 | 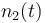
|
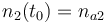
|
| Molar number 3 | 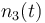
|
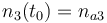
|
| Name | Symbol | Value |
| Molar Mass | 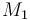
|
0.1362 |
| Molar Mass | 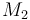
|
0.09806 |
| Molar Mass | 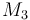
|
0.23426 |
| Molar Mass | 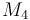
|
0.236 |
| Universal gas constant | 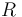
|
8.314 |
| Reference temperature | 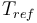
|
293 |
| Name | Symbol | Value |
| Steric factor | 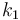
|
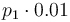
|
| Steric factor | 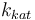
|
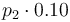
|
| Activation energie | 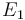
|
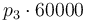
|
| Activation energie | 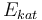
|
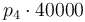
|
| Catalyst deactivation coefficient | 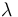
|
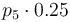
|
with 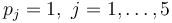
| Name | Symbol | Interval |
| Initial molar number 1 | 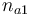
|
[0.4,9.0] |
| Initial molar number 2 | 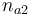
|
[0.4,9.0] |
| Initial molar number 3 | 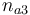
|
[0.4,9.0] |
| Concentration of the catalyst | 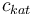
|
[0.0,6.0] |
| Initial molar number 1 | 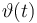
|
[20.0,100.0] |