Difference between revisions of "Category:Vanishing constraints"
JonasSchulze (Talk | contribs) m (Text replacement - "\<bibref\>(.*)\<\/bibref\>" to "<bib id="$1" />") |
JonasSchulze (Talk | contribs) m (Text replacement - "<bibreferences/>" to "<biblist />") |
||
| Line 14: | Line 14: | ||
== References == | == References == | ||
| − | < | + | <biblist /> |
[[Category:Objective characterization]] | [[Category:Objective characterization]] | ||
Latest revision as of 11:10, 23 January 2016
This category contains mathematical programs with vanishing constraints (MPVCs). The problem
![\begin{array}{llcl}
\displaystyle \min_{y} & & & \Phi(y) \\[1.5ex]
\mbox{s.t.} & 0 & \ge & g_i(y) h_i(y), \quad i \in \{1, \dots, m\}\\
& 0 & \le & \le h(y) \\
\end{array}](https://mintoc.de/images/math/e/3/4/e34bf81c680f860655fecd6237d2d2a2.png)
with smooth functions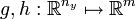 
is called MPVC. Note that every MPVC can be transformed into an MPEC [Achtziger2008]Author: W. Achtziger; C. Kanzow
Journal: Mathematical Programming Series A
Pages: 69--99
Title: Mathematical programs with vanishing constraints: optimality conditions and constraint qualifications
Volume: 114
Year: 2008
[Izmailov2009]Author: A.F. Izmailov; M.V. Solodov
Journal: Journal of Optimization Theory and Applications
Pages: 501--532
Title: Mathematical Programs with Vanishing Constraints: Optimality Conditions, Sensitivity, and a Relaxation Method
Volume: 142
Year: 2009. Examples for vanishing constraints are engine speed constraints that are only active if the corresponding gear control is nonzero.
References
| [Achtziger2008] | W. Achtziger; C. Kanzow (2008): Mathematical programs with vanishing constraints: optimality conditions and constraint qualifications. Mathematical Programming Series A, 114, 69--99 | |
| [Izmailov2009] | A.F. Izmailov; M.V. Solodov (2009): Mathematical Programs with Vanishing Constraints: Optimality Conditions, Sensitivity, and a Relaxation Method. Journal of Optimization Theory and Applications, 142, 501--532 | |
Pages in category "Vanishing constraints"
This category contains only the following page.
