Difference between revisions of "Category:Muscod"
FelixMueller (Talk | contribs) |
(Added description) |
||
| Line 1: | Line 1: | ||
| − | + | This category lists all problems that have a description of differential equations in MUSCOD-format. | |
| + | |||
| + | MUSCOD is an abbreviation for MUltiple Shooting COde for Direct Optimal Control. The original version was developed by Bock and Plitt in the 1980s and used in the seminal paper <bib id="Bock1984" /> which is often cited as the origin of the Direct Multiple Shooting method. The reimplementation MUSCOD-II by Daniel Leineweber in the 1990s is still the basis for ongoing development, in particular in the work groups of Georg Bock, Christian Kirches, Andreas Potschka (all Heidelberg), and Sebastian Sager (Magdeburg). MUSCOD-II is based on the direct multiple shooting method to treat multistage optimal control problems with DAE constraints. The extension MS-MINTOC by Sager is able to treat integrality requirements in an efficient way, compare <bib id="Sager2009" />. | ||
| + | |||
| + | For a standard MIOC written as | ||
| + | |||
| + | <p> | ||
| + | <math> | ||
| + | \begin{array}{llcl} | ||
| + | \displaystyle \min_{x(\cdot), u(\cdot), v(\cdot), q, \rho} & \phi(x(t_f), q, \rho) \\[1.5ex] | ||
| + | \mbox{s.t.} & \dot{x}(t) & = & f(x(t), u(t), v(t), q, \rho), \\ | ||
| + | & 0 &\le& c(x(t),u(t),v(t), q, \rho), \\[1.5ex] | ||
| + | & 0 &=& r^{\text{eq}}(x(t_0),x(t_1), \dots, x(t_m), q, \rho), \\ | ||
| + | & 0 &\le& r^{\text{ieq}}(x(t_0),x(t_1), \dots, x(t_m), q, \rho), \\[1.5ex] | ||
| + | & v(t) &\in& \Omega := \{v^1, v^2, \dots, v^{n_\omega} \},\\ | ||
| + | & \rho &\in& \Rho := \{\rho^1, \rho^2, \dots, \rho^{n_\Rho} \}, | ||
| + | \end{array} | ||
| + | </math> | ||
| + | </p> | ||
| + | |||
| + | the format looks, e.g., something like this: | ||
| + | <source lang="cpp"> | ||
| + | rhs[0] = xd[0] - xd[0]*xd[1] - p[0]*u[0]*xd[0]; | ||
| + | rhs[1] = - xd[1] + xd[0]*xd[1] - p[1]*u[0]*xd[1]; | ||
| + | </source> | ||
| + | |||
| + | for the special case | ||
| + | |||
| + | <p> | ||
| + | <math> | ||
| + | \begin{array}{llcl} | ||
| + | & \dot{x}_0(t) & = & x_0(t) - x_0(t) x_1(t) - \; c_0 x_0(t) \; w(t), \\ | ||
| + | & \dot{x}_1(t) & = & - x_1(t) + x_0(t) x_1(t) - \; c_1 x_1(t) \; w(t). | ||
| + | \end{array} | ||
| + | </math> | ||
| + | </p> | ||
| + | |||
| + | Here the vector entries ''rhs[i]'' contain the values of the right hand side function <math>f_i(\cdot)</math>. The vector entries ''xd[i]'' contains the differential variables <math>x_i(t)</math>, ''u[i]'' the control variables <math>u_i(t)</math> or <math>v_i(t)</math>, and ''p[i]'' contains the model parameters <math>p</math>or control differential variables <math>q_i(t)</math> resp. <math>\rho_i(t)</math>. | ||
== References == | == References == | ||
<biblist /> | <biblist /> | ||
| − | + | [[Category: Implementation]] | |
| − | + | ||
| − | + | ||
Latest revision as of 10:09, 28 January 2016
This category lists all problems that have a description of differential equations in MUSCOD-format.
MUSCOD is an abbreviation for MUltiple Shooting COde for Direct Optimal Control. The original version was developed by Bock and Plitt in the 1980s and used in the seminal paper [Bock1984]Address: Budapest
Author: H.G. Bock; K.J. Plitt
Booktitle: Proceedings of the 9th IFAC World Congress
Pages: 242--247
Publisher: Pergamon Press
Title: A Multiple Shooting algorithm for direct solution of optimal control problems
Url: http://www.iwr.uni-heidelberg.de/groups/agbock/FILES/Bock1984.pdf
Year: 1984 which is often cited as the origin of the Direct Multiple Shooting method. The reimplementation MUSCOD-II by Daniel Leineweber in the 1990s is still the basis for ongoing development, in particular in the work groups of Georg Bock, Christian Kirches, Andreas Potschka (all Heidelberg), and Sebastian Sager (Magdeburg). MUSCOD-II is based on the direct multiple shooting method to treat multistage optimal control problems with DAE constraints. The extension MS-MINTOC by Sager is able to treat integrality requirements in an efficient way, compare [Sager2009]Author: Sager, S.; Reinelt, G.; Bock, H.G.
which is often cited as the origin of the Direct Multiple Shooting method. The reimplementation MUSCOD-II by Daniel Leineweber in the 1990s is still the basis for ongoing development, in particular in the work groups of Georg Bock, Christian Kirches, Andreas Potschka (all Heidelberg), and Sebastian Sager (Magdeburg). MUSCOD-II is based on the direct multiple shooting method to treat multistage optimal control problems with DAE constraints. The extension MS-MINTOC by Sager is able to treat integrality requirements in an efficient way, compare [Sager2009]Author: Sager, S.; Reinelt, G.; Bock, H.G.
Journal: Mathematical Programming
Number: 1
Pages: 109--149
Title: Direct Methods With Maximal Lower Bound for Mixed-Integer Optimal Control Problems
Url: http://mathopt.de/PUBLICATIONS/Sager2009.pdf
Volume: 118
Year: 2009 .
.
For a standard MIOC written as
![\begin{array}{llcl}
\displaystyle \min_{x(\cdot), u(\cdot), v(\cdot), q, \rho} & \phi(x(t_f), q, \rho) \\[1.5ex]
\mbox{s.t.} & \dot{x}(t) & = & f(x(t), u(t), v(t), q, \rho), \\
& 0 &\le& c(x(t),u(t),v(t), q, \rho), \\[1.5ex]
& 0 &=& r^{\text{eq}}(x(t_0),x(t_1), \dots, x(t_m), q, \rho), \\
& 0 &\le& r^{\text{ieq}}(x(t_0),x(t_1), \dots, x(t_m), q, \rho), \\[1.5ex]
& v(t) &\in& \Omega := \{v^1, v^2, \dots, v^{n_\omega} \},\\
& \rho &\in& \Rho := \{\rho^1, \rho^2, \dots, \rho^{n_\Rho} \},
\end{array}](https://mintoc.de/images/math/c/2/e/c2ea6ba320c6ca71260f7eeb98105969.png)
the format looks, e.g., something like this:
rhs[0] = xd[0] - xd[0]*xd[1] - p[0]*u[0]*xd[0]; rhs[1] = - xd[1] + xd[0]*xd[1] - p[1]*u[0]*xd[1];
for the special case
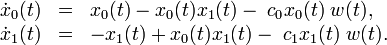
Here the vector entries rhs[i] contain the values of the right hand side function 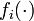 . The vector entries xd[i] contains the differential variables
. The vector entries xd[i] contains the differential variables 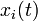 , u[i] the control variables
, u[i] the control variables 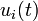 or
or 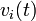 , and p[i] contains the model parameters
, and p[i] contains the model parameters 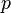 or control differential variables
or control differential variables 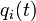 resp.
resp. 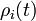 .
.
References
There were no citations found in the article.
Pages in category "Muscod"
The following 9 pages are in this category, out of 9 total.