Difference between revisions of "Control of Heat Equation with Actuator Placement"
FelixMueller (Talk | contribs) (→Discretization) |
FelixMueller (Talk | contribs) (→Parameters) |
||
| (21 intermediate revisions by the same user not shown) | |||
| Line 12: | Line 12: | ||
This problem is governed by the heat equation and is adapted from Iftime and Demetriou (<bib id="Iftime2009"/>). | This problem is governed by the heat equation and is adapted from Iftime and Demetriou (<bib id="Iftime2009"/>). | ||
Its goal is to choose a place to apply an actuator in a given area depending on time. | Its goal is to choose a place to apply an actuator in a given area depending on time. | ||
| − | The objective function is quadratic, its first term captures the desired final state <math>\bar{u}\equiv 0</math>, the second term | + | The objective function is quadratic, its first term captures the desired final state <math>\bar{u}\equiv 0</math>, the second term regularizes the state over time and the third term regularizes the continuous controls. |
The constraints are a source budget, which limits the quantity of placed actuators, and the two-dimensional heat equation with some source function. | The constraints are a source budget, which limits the quantity of placed actuators, and the two-dimensional heat equation with some source function. | ||
Additionally, we assume Dirichlet boundary conditions and initial conditions. | Additionally, we assume Dirichlet boundary conditions and initial conditions. | ||
Originally, the problem formulation was non-convex. | Originally, the problem formulation was non-convex. | ||
| − | We overcome this issue by substitution of <math>v(t)w_l(t)</math> by <math>v_l(t)</math> and adding the Big | + | We overcome this issue by substitution of <math>v(t)w_l(t)</math> by <math>v_l(t)</math> and adding the Big M formulation. |
== Mathematical formulation == | == Mathematical formulation == | ||
| − | |||
<p> | <p> | ||
<math> | <math> | ||
| − | \begin{array}{ | + | \begin{array}{lllcl} |
| − | \min\limits_{u,v,w}~~ & | + | \min\limits_{u,v,w}~~ &||u(t_f)||_{2,\Omega}^2 &+2||u||_{2,\Omega\times T}^2+\frac{1}{500}\sum\limits_{l=1}^L||v_l||^2_{2,T} & \\[10pt] |
| − | \text{ s.t.} ~~~~ &\frac{\partial u}{\partial t} | + | \text{ s.t.} ~~~~ &\frac{\partial u}{\partial t}- \kappa \Delta u & =\sum\limits_{l=1}^L v_l f_l &\text{ in }&\Omega\times T\\[10pt] |
| − | & u | + | & u & =0 &\text{ on } &\partial\Omega\times T \\[10pt] |
| − | & u(x,y,0) = 100 \sin(\pi x)\sin(\pi y) &\text{ in }& \Omega\\[10pt] | + | & u(x, y, 0) & = 100 \sin(\pi x)\sin(\pi y) &\text{ in }& \Omega\\[10pt] |
| − | & | + | & |v_l| & \leq M w_l \quad \forall l\in \{1,\dots,L\} &\text{ in } & T \\[10pt] |
| − | & \sum\limits_{l=1}^L w_l | + | & \sum\limits_{l=1}^L w_l & \leq W &\text{ in } & T\\[10pt] |
| − | & w_l(t)\in \{0,1\} \ | + | & w_l(t) & \in \{0,1\} \quad \forall l\in \{1,\dots,L\} &\text{ in } &T. |
\end{array} | \end{array} | ||
| Line 55: | Line 54: | ||
\begin{array}{rcl} | \begin{array}{rcl} | ||
\Omega &=& [0,1] \times [0,2],\\ | \Omega &=& [0,1] \times [0,2],\\ | ||
| + | T & = & [0, t_f], \\ | ||
| + | t_f &=&10,\\ | ||
\kappa &=& 0.01,\\ | \kappa &=& 0.01,\\ | ||
L &=& 9, \\ | L &=& 9, \\ | ||
W &=& 1,\\ | W &=& 1,\\ | ||
| − | |||
\varepsilon &=& 0.01 . | \varepsilon &=& 0.01 . | ||
\end{array} | \end{array} | ||
| Line 68: | Line 68: | ||
The source budget is limited by <math>W</math> and <math>t_f</math> denotes the final time. | The source budget is limited by <math>W</math> and <math>t_f</math> denotes the final time. | ||
| − | + | ==Discretization== | |
| − | To solve the problem we apply a "first discretize, then optimize" approach | + | |
| + | To solve the problem we apply a "first discretize, then optimize" approach and discretize the components of the problem. | ||
For the heat equation, we use a five-point-stencil in space and the implicit euler in time. | For the heat equation, we use a five-point-stencil in space and the implicit euler in time. | ||
For <math>i=1,\dots, N-1</math>, <math>j=1,\dots, M-1</math>, and <math>k=0,\dots, T_n-1</math>, this yields: | For <math>i=1,\dots, N-1</math>, <math>j=1,\dots, M-1</math>, and <math>k=0,\dots, T_n-1</math>, this yields: | ||
| − | + | <p> | |
<math> \frac{1}{h_t}(u_{i,j,k}-u_{i,j,k-1}) - \frac{\kappa_{i,j}}{h_x h_y}(u_{i-1,j,k}+u_{i+1,j,k}+u_{i,j-1,k}+u_{i,j+1,k}-4u_{i,j,k}) = \sum\limits_{l=1}^L(v_{k+1,l}+v_{k ,l} )f_l(ih_x,jh_y), </math> | <math> \frac{1}{h_t}(u_{i,j,k}-u_{i,j,k-1}) - \frac{\kappa_{i,j}}{h_x h_y}(u_{i-1,j,k}+u_{i+1,j,k}+u_{i,j-1,k}+u_{i,j+1,k}-4u_{i,j,k}) = \sum\limits_{l=1}^L(v_{k+1,l}+v_{k ,l} )f_l(ih_x,jh_y), </math> | ||
| − | + | </p> | |
| − | with <math>u_{i,j,k}=u(ih_x,jh_y,kh_t)</math>, the stepsizes <math>h_x,h_y</math> | + | with <math>u_{i,j,k}=u(ih_x,jh_y,kh_t)</math>,<math>v_{k ,l}=v_l(kh_t)</math>, <math>\kappa_{i,j}=\kappa(ih_x,jh_y)</math>, with the stepsizes in space <math>h_x,h_y</math>, and in time <math>h_t</math>, respectively. |
It holds for the source buget with the discretized binary controls <math>w_{l,k}</math> for all <math>k\in \{0,\dots,T_n\}</math>: | It holds for the source buget with the discretized binary controls <math>w_{l,k}</math> for all <math>k\in \{0,\dots,T_n\}</math>: | ||
| Line 82: | Line 83: | ||
This condition is called SOS-<math>W</math> conditon. | This condition is called SOS-<math>W</math> conditon. | ||
| − | We remark that the number of discretized binary variables does not depend on the space discretization but | + | We remark that the number of discretized binary variables does not depend on the space discretization but does on the time discretization. That is why we tagged this problem as containing mesh-independent and mesh-dependent integer variables. |
| + | |||
| + | ==Reference Solution== | ||
==Source Code== | ==Source Code== | ||
| Line 94: | Line 97: | ||
<!--List of all categories this page is part of. List characterization of solution behavior, model properties, ore presence of implementation details (e.g., AMPL for AMPL model) here --> | <!--List of all categories this page is part of. List characterization of solution behavior, model properties, ore presence of implementation details (e.g., AMPL for AMPL model) here --> | ||
[[Category:MIOCP]] | [[Category:MIOCP]] | ||
| + | [[Category:PDE model]] | ||
| + | [[Category:Parabolic]] | ||
| + | [[Category:Tracking objective]] | ||
| + | [[Category:Mesh-dependent integer variables]] | ||
| + | [[Category:Mesh-independent integer variables]] | ||
Latest revision as of 11:52, 7 March 2016
| Control of Heat Equation with Actuator Placement | |
|---|---|
| State dimension: | 1 |
| Differential states: | 1 |
| Continuous control functions: | 9 |
| Discrete control functions: | 9 |
| Path constraints: | 3 |
| Interior point equalities: | 2 |
This problem is governed by the heat equation and is adapted from Iftime and Demetriou ([Iftime2009]Author: Orest V. Iftime; Michael A. Demetriou
Journal: {A}utomatica
Number: 2
Pages: 312--323
Title: {O}ptimal control of switched distributed parameter systems with spatially scheduled actuators
Volume: 45
Year: 2009 ).
Its goal is to choose a place to apply an actuator in a given area depending on time.
The objective function is quadratic, its first term captures the desired final state
).
Its goal is to choose a place to apply an actuator in a given area depending on time.
The objective function is quadratic, its first term captures the desired final state 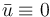 , the second term regularizes the state over time and the third term regularizes the continuous controls.
The constraints are a source budget, which limits the quantity of placed actuators, and the two-dimensional heat equation with some source function.
Additionally, we assume Dirichlet boundary conditions and initial conditions.
Originally, the problem formulation was non-convex.
We overcome this issue by substitution of
, the second term regularizes the state over time and the third term regularizes the continuous controls.
The constraints are a source budget, which limits the quantity of placed actuators, and the two-dimensional heat equation with some source function.
Additionally, we assume Dirichlet boundary conditions and initial conditions.
Originally, the problem formulation was non-convex.
We overcome this issue by substitution of 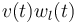 by
by 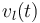 and adding the Big M formulation.
and adding the Big M formulation.
Contents
Mathematical formulation
![\begin{array}{lllcl}
\min\limits_{u,v,w}~~ &||u(t_f)||_{2,\Omega}^2 &+2||u||_{2,\Omega\times T}^2+\frac{1}{500}\sum\limits_{l=1}^L||v_l||^2_{2,T} & \\[10pt]
\text{ s.t.} ~~~~ &\frac{\partial u}{\partial t}- \kappa \Delta u & =\sum\limits_{l=1}^L v_l f_l &\text{ in }&\Omega\times T\\[10pt]
& u & =0 &\text{ on } &\partial\Omega\times T \\[10pt]
& u(x, y, 0) & = 100 \sin(\pi x)\sin(\pi y) &\text{ in }& \Omega\\[10pt]
& |v_l| & \leq M w_l \quad \forall l\in \{1,\dots,L\} &\text{ in } & T \\[10pt]
& \sum\limits_{l=1}^L w_l & \leq W &\text{ in } & T\\[10pt]
& w_l(t) & \in \{0,1\} \quad \forall l\in \{1,\dots,L\} &\text{ in } &T.
\end{array}](https://mintoc.de/images/math/f/7/b/f7b975ab83d9bb58b11ac0ba6e8f87bb.png)
Parameters
We define the source term for all locations 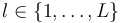 and a
fix parameter
and a
fix parameter 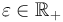 :
:
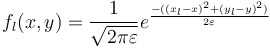 where
where 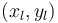 is the coordinate of the mesh point of the
is the coordinate of the mesh point of the 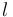 th possible actuator location.
th possible actuator location.
The parameters used are:
![\begin{array}{rcl}
\Omega &=& [0,1] \times [0,2],\\
T & = & [0, t_f], \\
t_f &=&10,\\
\kappa &=& 0.01,\\
L &=& 9, \\
W &=& 1,\\
\varepsilon &=& 0.01 .
\end{array}](https://mintoc.de/images/math/8/8/8/8887ac63da680738abdd4d737f46d8d7.png)
The parameter 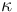 describes the thermal dissipativity of the material in the domain
describes the thermal dissipativity of the material in the domain 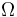 , it may vary in space:
, it may vary in space: 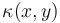 .
The parameter
.
The parameter 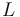 indicates the number of possible actuator locations. They are distributed as indicated in the picture.
The source budget is limited by
indicates the number of possible actuator locations. They are distributed as indicated in the picture.
The source budget is limited by 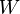 and
and 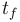 denotes the final time.
denotes the final time.
Discretization
To solve the problem we apply a "first discretize, then optimize" approach and discretize the components of the problem.
For the heat equation, we use a five-point-stencil in space and the implicit euler in time.
For 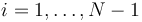 ,
,  , and
, and  , this yields:
, this yields:
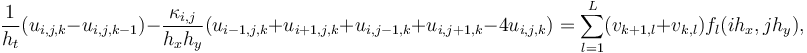
with 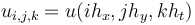 ,
,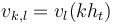 ,
, 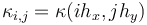 , with the stepsizes in space
, with the stepsizes in space 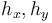 , and in time
, and in time 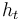 , respectively.
, respectively.
It holds for the source buget with the discretized binary controls 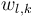 for all
for all 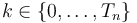 :
:
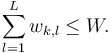
This condition is called SOS-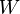 conditon.
conditon.
We remark that the number of discretized binary variables does not depend on the space discretization but does on the time discretization. That is why we tagged this problem as containing mesh-independent and mesh-dependent integer variables.
Reference Solution
Source Code
References
| [Iftime2009] | Orest V. Iftime; Michael A. Demetriou (2009): {O}ptimal control of switched distributed parameter systems with spatially scheduled actuators . {A}utomatica, 45, 312--323 |  |