Difference between revisions of "Category:Boolean variables"
m (Initial setup of IMA paper text) |
JonasSchulze (Talk | contribs) m (Text replacement - "<bibreferences/>" to "<biblist />") |
||
| (One intermediate revision by the same user not shown) | |||
| Line 2: | Line 2: | ||
<center><math>\delta_i: [0, t_f] \mapsto \{ \mathrm{true}, \mathrm{false} \}</math></center> | <center><math>\delta_i: [0, t_f] \mapsto \{ \mathrm{true}, \mathrm{false} \}</math></center> | ||
| − | that indicate whether a model formulation <math>F_i[x,u,v]</math> is active at time <math>t</math>, both state-dependent switches and outer convexification formulations may be written as ''disjunctive programs'', i.e., optimization problems involving Boolean variables and logical conditions. Using disjunctive programs can be seen as a more natural way of modeling discrete events and has the main advantage of resulting in tighter relaxations of the discrete dicisions, when compared to integer programming techniques. More details can be found, e.g., in < | + | that indicate whether a model formulation <math>F_i[x,u,v]</math> is active at time <math>t</math>, both state-dependent switches and outer convexification formulations may be written as ''disjunctive programs'', i.e., optimization problems involving Boolean variables and logical conditions. Using disjunctive programs can be seen as a more natural way of modeling discrete events and has the main advantage of resulting in tighter relaxations of the discrete dicisions, when compared to integer programming techniques. More details can be found, e.g., in <bib id="Grossmann2002" /><bib id="Oldenburg2005" /><bib id="Oldenburg2008" />. |
== References == | == References == | ||
| − | < | + | <biblist /> |
[[Category:Model characterization]] | [[Category:Model characterization]] | ||
Latest revision as of 11:10, 23 January 2016
Discrete switching events can also be expressed by means of Boolean variables and logical implications. E.g., by introducing logical functions
![\delta_i: [0, t_f] \mapsto \{ \mathrm{true}, \mathrm{false} \}](https://mintoc.de/images/math/1/2/f/12f0eb048533d6e0735023f25291eb9a.png)
that indicate whether a model formulation ![F_i[x,u,v]](https://mintoc.de/images/math/3/0/0/300379516af3af3001dc366fb69a9c28.png)
is active at time 
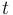, both state-dependent switches and outer convexification formulations may be written as disjunctive programs, i.e., optimization problems involving Boolean variables and logical conditions. Using disjunctive programs can be seen as a more natural way of modeling discrete events and has the main advantage of resulting in tighter relaxations of the discrete dicisions, when compared to integer programming techniques. More details can be found, e.g., in [Grossmann2002]Author: I.E. Grossmann
Journal: Optimization and Engineering
Pages: 227--252
Title: Review of Nonlinear Mixed-Integer and Disjunctive Programming Techniques
Volume: 3
Year: 2002
[Oldenburg2005]Address: D\"usseldorf
Author: J. Oldenburg
Publisher: VDI Verlag
Series: Fortschritt-Berichte VDI Reihe 3, Verfahrens\-technik
Title: Logic--based modeling and optimization of discrete--continuous dynamic systems
Volume: 830
Year: 2005[Oldenburg2008]Author: J. Oldenburg; W. Marquardt
Journal: Computers \& Chemical Engineering
Number: 10
Pages: 2346--2364
Title: Disjunctive modeling for optimal control of hybrid systems
Volume: 32
Year: 2008.
References
There were no citations found in the article.
This category currently contains no pages or media.
