Difference between revisions of "Goddart's rocket problem"
From mintOC
| Line 49: | Line 49: | ||
</math> | </math> | ||
</dd> | </dd> | ||
| + | |||
| + | == Reference Solution == | ||
| + | |||
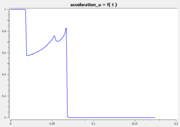
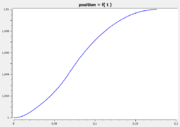
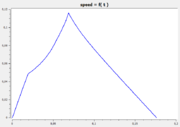
| + | The following reference solution was generated using BOCOP. The optimal value of the objective function is -0.63389. | ||
| + | |||
| + | |||
| + | <gallery caption="Reference solution plots" widths="180px" heights="140px" perrow="2"> | ||
| + | Image:Goddartacc.png| Control u over time. | ||
| + | Image:Goddartpos.png| Position r over time. | ||
| + | Image:Goddartspeed.png| Speed v over time. | ||
| + | Image:Goddartmass.png| Mass m over time. | ||
| + | </gallery> | ||
Revision as of 14:27, 14 January 2016
In Goddart's rocket problem we model the ascent (vertical; restricted to 1 dimension) of a rocket. The aim is to reach a certain altitude with minimal fuel consumption. It is equivalent to maximize the mass at the final altitude.
Variables
The state variables 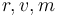 describe the altitude, speed and mass.
describe the altitude, speed and mass.
The drag is given by
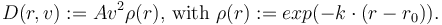
Mathematical formulation
![\begin{array}{llcll}
\displaystyle \max_{m,r,v,u,T} & m(T)\\[1.5ex]
\mbox{s.t.} & \dot{r} & = & v, \\
& \dot{v} & = & -\frac{1}{r^2} + \frac{1}{m} (T_{max}u-D(r,v)) \\[1.5ex]
& \dot{m} & = & -b T_{max} u, \\
& u(\cdot) &\in& [0,1] \\
& r(0) &=& r_0, \\
& v(0) &=& v_0, \\
& m(0) &=& m_0, \\
& r(T) &=& r_T, \\
& D(r(\cdot),v(\cdot))&\le& C \\
& T free
\end{array}](https://mintoc.de/images/math/5/3/d/53db547e29a6f4c48cfc15c1ba7137b5.png)
Parameters
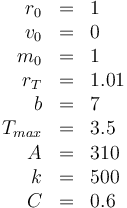
Reference Solution
The following reference solution was generated using BOCOP. The optimal value of the objective function is -0.63389.
- Reference solution plots