Difference between revisions of "Category:Parabolic"
From mintOC
FelixMueller (Talk | contribs) |
FelixMueller (Talk | contribs) |
||
| Line 4: | Line 4: | ||
<math>\sum^n_{i,j=1} a_{ij} \frac{\partial^2u}{\partial x_i \partial x_j} +\, \text{lower-order terms} = 0</math>. </p> | <math>\sum^n_{i,j=1} a_{ij} \frac{\partial^2u}{\partial x_i \partial x_j} +\, \text{lower-order terms} = 0</math>. </p> | ||
| − | + | ||
If <math>A=(a_{ij})_{ij}</math> is positive or negative semidefinite with exact one eigenvalue zero, the partial differential equation is called parabolic. | If <math>A=(a_{ij})_{ij}</math> is positive or negative semidefinite with exact one eigenvalue zero, the partial differential equation is called parabolic. | ||
Revision as of 16:20, 24 February 2016
This category contains all control problems which are governed by a parabolic partial differential equation.
A second order linear partial differential equation can be written as
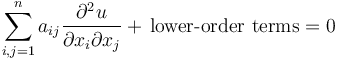 .
.
Ifis positive or negative semidefinite with exact one eigenvalue zero, the partial differential equation is called parabolic. An example is the heat equation:
, where
denotes the Laplace operator,
is the unknown, and the function
is given. </p>
Pages in category "Parabolic"
This category contains only the following page.