Difference between revisions of "Annihilation of calcium oscillations"

From mintOC
Jump to: navigation, search
m (Added long time behavior)
m (Added objective function landscape)
Line 3: Line 3:
 
|nx        = 4
 
|nx        = 4
 
|nw        = 1
 
|nw        = 1
−
|nre      = 3
+
|nre      = 4
 
}}
 
}}
  
 
The aim of the control problem is to identify strength and timing of inhibitor stimuli that lead to a phase singularity which annihilates intracellular calcium oscillations. This is formulated as an objective function that aims at minimizing the state deviation from a desired unstable steady state, integrated over time.
 
The aim of the control problem is to identify strength and timing of inhibitor stimuli that lead to a phase singularity which annihilates intracellular calcium oscillations. This is formulated as an objective function that aims at minimizing the state deviation from a desired unstable steady state, integrated over time.
 +
 +
The mathematical equations form a small-scale [[:Category:ODE model|ODE model]]. The interior point equality conditions fix the initial values of the differential states. The problem is, despite of its low dimension, very hard to solve, as the target state is [[:Category:Unstable | unstable]].
 +
 +
== Biological motivation ==
  
 
Biological rhythms as impressing manifestations of self-organized dynamics associated with the phenomenon life have been of particular interest since quite a long time. Even before the mechanistic basis of certain biochemical oscillators was elucidated by molecular biology techniques, their investigation and the issue of perturbation by external stimuli has attracted much attention.
 
Biological rhythms as impressing manifestations of self-organized dynamics associated with the phenomenon life have been of particular interest since quite a long time. Even before the mechanistic basis of certain biochemical oscillators was elucidated by molecular biology techniques, their investigation and the issue of perturbation by external stimuli has attracted much attention.
Line 13: Line 17:
  
 
As a source of external control a temporally varying concentration of an uncompetitive inhibitor of the PMCA ion pump is considered.
 
As a source of external control a temporally varying concentration of an uncompetitive inhibitor of the PMCA ion pump is considered.
−
 
−
The mathematical equations form a small-scale [[:Category:ODE model|ODE model]]. The interior point equality conditions fix the initial values of the differential states. The problem is, despite of its low dimension, very hard to solve, as the target state is [[:Category:Unstable | unstable]].
 
  
 
== Mathematical formulation ==
 
== Mathematical formulation ==
Line 79: Line 81:
 
  Image:calciumStatesLongTime.png| Long time behavior of optimal solution: numerical rounding errors lead to transition back from unstable steady-state to stable limit-cycle.
 
  Image:calciumStatesLongTime.png| Long time behavior of optimal solution: numerical rounding errors lead to transition back from unstable steady-state to stable limit-cycle.
 
</gallery>
 
</gallery>
−
 
  
 
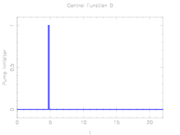
The depicted optimal solution consists of a stimulus of <math>w^{\mathrm{max}}=1.3</math> and a timing given by the stage lengths 4.6947115251487972, 0.14910388207934536, and 17.156184592771854. As can be seen from the additional plots, this solution is extremely unstable. A small perturbation in the control, or simply rounding errors on a longer time horizon lead to a transition back to the stable limit-cycle oscillations.
 
The depicted optimal solution consists of a stimulus of <math>w^{\mathrm{max}}=1.3</math> and a timing given by the stage lengths 4.6947115251487972, 0.14910388207934536, and 17.156184592771854. As can be seen from the additional plots, this solution is extremely unstable. A small perturbation in the control, or simply rounding errors on a longer time horizon lead to a transition back to the stable limit-cycle oscillations.
 +
 +
== Optimization ==
 +
 +
The determination of the stimulus by means of optimization is quite hard for two reasons. First, the unstable target steady-state. Only a stable all-at-once algorithm such as multiple shooting or collocation can be applied successfully.
 +
 +
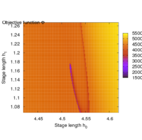
Second, the objective landscape of the problem in switching time formulation (this is, for a fixed stimulus strength and modifying only beginning and length of the stimulus) is quite nasty, as the following visualizations obtained by simulation show.
 +
 +
<gallery caption="Objective landscape simulation plots" widths="180px" heights="140px" perrow="2">
 +
Image:calciumObjectiveSimulation1.png| Brute-force simulation of objective landscape for different values of stimulus beginning and length.
 +
Image:calciumObjectiveSimulation2.png| Zoom in.
 +
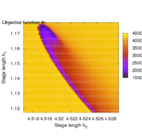
Image:calciumObjectiveSimulation3.png| Zoom in.
 +
Image:calciumObjectiveSimulation4.png| Note that the border line of the small channel is a local maximum, hence an initialization slightly away will not lead to the correct global minimum.
 +
</gallery>
 +
  
 
== Source Code ==
 
== Source Code ==

Revision as of 15:30, 12 November 2008

Annihilation of calcium oscillations
State dimension: 1
Differential states: 4
Discrete control functions: 1
Interior point equalities: 4


The aim of the control problem is to identify strength and timing of inhibitor stimuli that lead to a phase singularity which annihilates intracellular calcium oscillations. This is formulated as an objective function that aims at minimizing the state deviation from a desired unstable steady state, integrated over time.

The mathematical equations form a small-scale ODE model. The interior point equality conditions fix the initial values of the differential states. The problem is, despite of its low dimension, very hard to solve, as the target state is unstable.

Biological motivation

Biological rhythms as impressing manifestations of self-organized dynamics associated with the phenomenon life have been of particular interest since quite a long time. Even before the mechanistic basis of certain biochemical oscillators was elucidated by molecular biology techniques, their investigation and the issue of perturbation by external stimuli has attracted much attention.

A calcium oscillator model describing intracellular calcium spiking in hepatocytes induced by an extracellular increase in adenosine triphosphate (ATP) concentration is described. The calcium signaling pathway is initiated via a receptor activated G-protein inducing the intracellular release of inositol triphoshate (IP3) by phospholipase C. The IP3 triggers the opening of endoplasmic reticulum and plasma membrane calcium channels and a subsequent inflow of calcium ions from intracellular and extracellular stores leading to transient calcium spikes.

As a source of external control a temporally varying concentration of an uncompetitive inhibitor of the PMCA ion pump is considered.

Mathematical formulation

For t \in [t_0, t_f] almost everywhere the mixed-integer optimal control problem is given by

\begin{array}{llcl} \displaystyle \min_{x, w, w^{\mathrm{max}}} & & & {\int_{t_0}^{t_f} || x(\tau) - \tilde{x} ||_2^2 \; \mathrm{d}\tau} \\[1.5ex] \mbox{s.t.} & \dot{x}_0 & = & k_1 + k_2 x_0 - \frac{k_3 x_0 x_1}{x_0 + K_4} - \frac{k_5 x_0 x_2}{x_0 + K_6} \\ & \dot{x}_1 & = & k_7 x_0 - \frac{k_8 x_1}{x_1 + K_9} \\ & \dot{x}_2 & = & \frac{k_{10} x_1 x_2 x_3}{x_3 + K_{11}} + k_{12} x_1 + k_{13} x_0 - \frac{k_{14} x_2}{{w} x_2 + K_{15}} - \frac{k_{16} x_2}{x_2 + K_{17}} + \frac{x_3}{10} \\ & \dot{x}_3 & = & - \frac{k_{10} x_1 x_2 x_3}{x_3 + K_{11}} + \frac{k_{16} x_2}{x_2 + K_{17}} - \frac{x_3}{10} \\[1.5ex] & x(0) &=& (0.03966, 1.09799, 0.00142, 1.65431)^T, \\ & x(t) & \ge & 0.0, \\ & w(t) &\in& \{0, w^{\mathrm{max}}\}, \\ & w^{\mathrm{max}} & \ge & 1.1, \\ & w^{\mathrm{max}} & \le & 1.3. \end{array}

Here the differential states 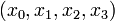(x_0, x_1, x_2, x_3) describe concentrations of activated G-proteins, active phospholipase C, intracellular calcium, and intra-ER calcium, respectively.

Modeling details including a comprehensive discussion of parameter values and the dynamical behavior observed in simulations with a comparison to experimental observations can be found in <bibref>Kummer2000</bibref>. In the given equations that stem from <bibref>Lebiedz2005</bibref>, the model is identical to the one derived there, except for an additional first-order leakage flow of calcium from the ER back to the cytoplasm, which is modeled by 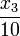\frac{x_3}{10} in equations 3 and 4. It reproduces well experimental observations of cytoplasmic calcium oscillations as well as bursting behavior and in particular the frequency encoding of the triggering stimulus strength, which is a well known mechanism for signal processing in cell biology.

Parameters

These fixed values are used within the model.

\begin{array}{rcl} [t_0, t_f] &=& [0, 22],\\ k_1 &=& 0.09, \\ k_2 &=& 2.30066, \\ k_3 &=& 0.64, \\ K_4 &=& 0.19, \\ k_5 &=& 4.88, \\ K_6 &=& 1.18, \\ k_7 &=& 2.08, \\ k_8 &=& 32.24, \\ K_9 &=& 29.09, \\ k_{10} &=& 5.0, \\ K_{11} &=& 2.67, \\ k_{12} &=& 0.7, \\ k_{13} &=& 13.58, \\ k_{14} &=& 153.0, \\ K_{15} &=& 0.16, \\ k_{16} &=& 4.85, \\ K_{17} &=& 0.05, \\ p_1 &=& 100, \\ p_2 &=& 5, \\ \tilde{x}_0 &=& 6.78677, \\ \tilde{x}_1 &=& 22.65836, \\ \tilde{x}_2 &=& 0.384306, \\ \tilde{x}_3 &=& 0.28977. \end{array}

Reference Solutions

  • Reference solution plots

  • Optimal stimuli determined by mixed-integer optimal control.

  • Corresponding differential states.

  • Slightly perturbed control: stimulus 0.001 too early.

  • Long time behavior of optimal solution: numerical rounding errors lead to transition back from unstable steady-state to stable limit-cycle.

The depicted optimal solution consists of a stimulus of 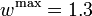w^{\mathrm{max}}=1.3 and a timing given by the stage lengths 4.6947115251487972, 0.14910388207934536, and 17.156184592771854. As can be seen from the additional plots, this solution is extremely unstable. A small perturbation in the control, or simply rounding errors on a longer time horizon lead to a transition back to the stable limit-cycle oscillations.

Optimization

The determination of the stimulus by means of optimization is quite hard for two reasons. First, the unstable target steady-state. Only a stable all-at-once algorithm such as multiple shooting or collocation can be applied successfully.

Second, the objective landscape of the problem in switching time formulation (this is, for a fixed stimulus strength and modifying only beginning and length of the stimulus) is quite nasty, as the following visualizations obtained by simulation show.

  • Objective landscape simulation plots

  • Brute-force simulation of objective landscape for different values of stimulus beginning and length.

  • Zoom in.

  • Zoom in.

  • Note that the border line of the small channel is a local maximum, hence an initialization slightly away will not lead to the correct global minimum.


Source Code

C

The differential equations in C code: 

double myu = p[17] * (1.0 + u[0]* ( p[19] - 1.0) ) ;
 
rhs[0] = p[0]
         + p[1]*xd[0]
         - p[2]*xd[0]*xd[1]/(xd[0]+p[3])
         - p[4]*xd[0]*xd[2]/(xd[0]+p[5]);
 
rhs[1] = p[6]*xd[0]
         - p[7]*xd[1]/(xd[1]+p[8]);
 
rhs[2] = p[9]*xd[1]*xd[2]*xd[3]/(xd[3]+p[10])
         + p[18]*p[11]*xd[1]
         + p[12]*xd[0]
         - p[13]*xd[2]/(myu*xd[2]+p[14])
         - p[15]*xd[2]/(xd[2]+p[16])
         + 0.1*xd[3];
 
rhs[3] = -p[9]*xd[1]*xd[2]*xd[3]/(xd[3]+p[10])
         + p[15]*xd[2]/(xd[2]+p[16])
         - 0.1*xd[3];

Variants

Use of two control functions.

References

<bibreferences/>

Retrieved from "https://mintoc.de/index.php?title=Annihilation_of_calcium_oscillations&oldid=256"