Difference between revisions of "Double Tank"
ClemensZeile (Talk | contribs) |
ClemensZeile (Talk | contribs) |
||
| Line 1: | Line 1: | ||
| + | {{Dimensions | ||
| + | |nd = 1 | ||
| + | |nx = 2 | ||
| + | |nu = 0 | ||
| + | |nw = 1 | ||
| + | |nre = 2 | ||
| + | }} | ||
| − | The double tank problem is a basic example for a switching system. It contains the dynamics of an upper and a lower tank, connected to each other with a pipe. The goal is to minimize the deviation of a certain fluid level <math>k_2</math> in the lower tank. | + | The double tank problem is a basic example for a switching system. It contains the dynamics of an upper and a lower tank, connected to each other with a pipe. The goal is to minimize the deviation of a certain fluid level <math>k_2</math> in the lower tank. The problem was introduced and discussed in a variety of publications for the optimal control of constrained switched systems, e.g. [http://homepages.laas.fr/henrion/papers/switch.pdf Henrion et al.] and [http://epubs.siam.org/doi/pdf/10.1137/120901507 Vasudevan et al.] |
== Mathematical formulation == | == Mathematical formulation == | ||
<math> | <math> | ||
| − | \begin{array}{ | + | \begin{array}{lll} |
| − | \displaystyle \min_{\sigma} & \displaystyle \int_{0}^{T}k_1(x_2-k_2)^2 \; \text{d}t \\[1.5ex] | + | \displaystyle \min_{\sigma} & \displaystyle \int_{0}^{T}k_1(x_2-k_2)^2 \; \text{d}t &\\[1.5ex] |
| − | \mbox{s.t.} & \displaystyle \dot{x}_1(t) = c_{\sigma(t)}-\sqrt{x_1(t)}, \\[1.5ex] | + | \mbox{s.t.} & \displaystyle \dot{x}_1(t) = c_{\sigma(t)}-\sqrt{x_1(t)} \qquad &\text{for } t\in[0,T], \\[1.5ex] |
| − | & \displaystyle \dot{x}_2(t) = \sqrt{x_2(t)}-\sqrt{x_2(t)} , \\[1.5ex] | + | & \displaystyle \dot{x}_2(t) = \sqrt{x_2(t)}-\sqrt{x_2(t)} \qquad &\text{for } t\in[0,T], \\[1.5ex] |
| − | & \displaystyle | + | & \displaystyle x_i(0)=x_{i0} \qquad &\text{for } i=1,2, \\[1.5ex] |
| − | & \displaystyle \sigma \in \{1,2\} | + | & \displaystyle \sigma(t) \in \{1,2\} \qquad &\text{for } t\in[0,T],\\[1.5ex] |
| − | + | ||
\end{array} | \end{array} | ||
</math> | </math> | ||
| − | |||
| Line 20: | Line 25: | ||
The two states of the system correspond to the fluid levels of an upper and a lower tank. | The two states of the system correspond to the fluid levels of an upper and a lower tank. | ||
The output of the upper tank flows into the lower tank, the output of the lower | The output of the upper tank flows into the lower tank, the output of the lower | ||
| − | tank exits the system, and the flow into the upper tank is restricted to either | + | tank exits the system, and the flow into the upper tank is restricted to either <math>c_1</math> [lt/s] |
| − | or | + | or <math>c_2</math> [lt/s]. The dynamics in each mode are then derived using [https://en.wikipedia.org/wiki/Torricelli's_law Torricelli’s law], as |
| − | shown in | + | shown in constraints 1 and 2. The objective of the optimization is to have the fluid level in the |
| − | lower tank equal to | + | lower tank equal to <math>k_2</math> [m], as reflected in the cost function. |
== Parameters == | == Parameters == | ||
| + | In an exemplary test, the parameters were chosen to be: | ||
<math>k_1=2, k_2=3, x_0=(2,2)',</math> with data <math>c_1=1</math> and <math>c_2=2</math>. | <math>k_1=2, k_2=3, x_0=(2,2)',</math> with data <math>c_1=1</math> and <math>c_2=2</math>. | ||
| + | <math>T=10</math> | ||
== Reference Solution == | == Reference Solution == | ||
| − | By introducing the lifts <math>l_i=\sqrt{x_i}</math> , algebraically constrained as <math>l_i^2=x_i, \; l_i\geq 0,</math> the problem is | + | By introducing the lifts <math>l_i=\sqrt{x_i}</math>, algebraically constrained as <math>l_i^2=x_i, \; l_i\geq 0,</math> the problem is recast with polynomial data. In this way way switch in connection with GloptiPoly3 can be applied. |
| + | |||
| + | |||
| + | == Source Code == | ||
| + | |||
| + | With the parameters above, the optimal control problem was tested using the following code. | ||
| + | |||
| + | == References == | ||
Revision as of 16:02, 10 December 2015
| Double Tank | |
|---|---|
| State dimension: | 1 |
| Differential states: | 2 |
| Continuous control functions: | 0 |
| Discrete control functions: | 1 |
| Interior point equalities: | 2 |
The double tank problem is a basic example for a switching system. It contains the dynamics of an upper and a lower tank, connected to each other with a pipe. The goal is to minimize the deviation of a certain fluid level 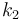 in the lower tank. The problem was introduced and discussed in a variety of publications for the optimal control of constrained switched systems, e.g. Henrion et al. and Vasudevan et al.
in the lower tank. The problem was introduced and discussed in a variety of publications for the optimal control of constrained switched systems, e.g. Henrion et al. and Vasudevan et al.
Mathematical formulation
![\begin{array}{lll}
\displaystyle \min_{\sigma} & \displaystyle \int_{0}^{T}k_1(x_2-k_2)^2 \; \text{d}t &\\[1.5ex]
\mbox{s.t.} & \displaystyle \dot{x}_1(t) = c_{\sigma(t)}-\sqrt{x_1(t)} \qquad &\text{for } t\in[0,T], \\[1.5ex]
& \displaystyle \dot{x}_2(t) = \sqrt{x_2(t)}-\sqrt{x_2(t)} \qquad &\text{for } t\in[0,T], \\[1.5ex]
& \displaystyle x_i(0)=x_{i0} \qquad &\text{for } i=1,2, \\[1.5ex]
& \displaystyle \sigma(t) \in \{1,2\} \qquad &\text{for } t\in[0,T],\\[1.5ex]
\end{array}](https://mintoc.de/images/math/b/f/1/bf130a0c53967bbbbe3baa830c510a61.png)
The two states of the system correspond to the fluid levels of an upper and a lower tank.
The output of the upper tank flows into the lower tank, the output of the lower
tank exits the system, and the flow into the upper tank is restricted to either 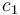 [lt/s]
or
[lt/s]
or 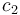 [lt/s]. The dynamics in each mode are then derived using Torricelli’s law, as
shown in constraints 1 and 2. The objective of the optimization is to have the fluid level in the
lower tank equal to
[lt/s]. The dynamics in each mode are then derived using Torricelli’s law, as
shown in constraints 1 and 2. The objective of the optimization is to have the fluid level in the
lower tank equal to 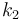 [m], as reflected in the cost function.
[m], as reflected in the cost function.
Parameters
In an exemplary test, the parameters were chosen to be:
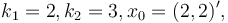 with data
with data 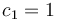 and
and 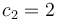 .
.
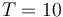
Reference Solution
By introducing the lifts 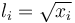 , algebraically constrained as
, algebraically constrained as 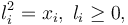 the problem is recast with polynomial data. In this way way switch in connection with GloptiPoly3 can be applied.
the problem is recast with polynomial data. In this way way switch in connection with GloptiPoly3 can be applied.
Source Code
With the parameters above, the optimal control problem was tested using the following code.