Difference between revisions of "Goddart's rocket problem"
From mintOC
FelixMueller (Talk | contribs) (→Mathematical formulation) |
FelixMueller (Talk | contribs) (→Mathematical formulation) |
||
| Line 21: | Line 21: | ||
& \dot{v}(t) & = & -\frac{1}{r(t)^2} + \frac{1}{m(t)} (T_{max}u(t)-D(r,v)) \\[1.5ex] | & \dot{v}(t) & = & -\frac{1}{r(t)^2} + \frac{1}{m(t)} (T_{max}u(t)-D(r,v)) \\[1.5ex] | ||
& \dot{m}(t) & = & -b T_{max} u(t), \\ | & \dot{m}(t) & = & -b T_{max} u(t), \\ | ||
| − | & u( | + | & u(t) &\in& [0,1] \\ |
& r(0) &=& r_0, \\ | & r(0) &=& r_0, \\ | ||
& v(0) &=& v_0, \\ | & v(0) &=& v_0, \\ | ||
Revision as of 12:07, 19 January 2016
In Goddart's rocket problem we model the ascent (vertical; restricted to 1 dimension) of a rocket. The aim is to reach a certain altitude with minimal fuel consumption. It is equivalent to maximize the mass at the final altitude.
Variables
The state variables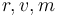 
describe the altitude(radius), speed and mass.
The drag is given by
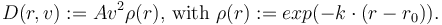
Mathematical formulation
![\begin{array}{llcll}
\displaystyle \min_{m,r,v,u,T} & -m(T)\\[1.5ex]
\mbox{s.t.} & \dot{r}(t) & = & v, \\
& \dot{v}(t) & = & -\frac{1}{r(t)^2} + \frac{1}{m(t)} (T_{max}u(t)-D(r,v)) \\[1.5ex]
& \dot{m}(t) & = & -b T_{max} u(t), \\
& u(t) &\in& [0,1] \\
& r(0) &=& r_0, \\
& v(0) &=& v_0, \\
& m(0) &=& m_0, \\
& r(T) &=& r_T, \\
& D(r(\cdot),v(\cdot))&\le& C \\
& T free
\end{array}](https://mintoc.de/images/math/5/4/d/54db1fed4baf51ddb6fa38ec0de79fee.png)
Parameters
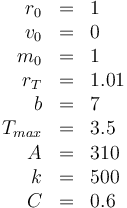
Reference Solution
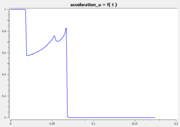
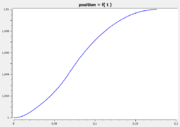
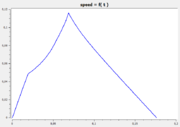
The following reference solution was generated using BOCOP. The optimal value of the objective function is -0.63389.
- Reference solution plots
Control u over time.
Position r over time.
Speed v over time.
Mass m over time.
References
The Problem can be found in the BOCOP User Guide.
