Difference between revisions of "Control of Heat Equation with Actuator Placement"
FelixMueller (Talk | contribs) (→Parameters) |
FelixMueller (Talk | contribs) (→Parameters) |
||
| Line 47: | Line 47: | ||
\kappa &=& 0.01. | \kappa &=& 0.01. | ||
\end{array} | \end{array} | ||
| − | </math> | + | </math>\\ |
The parameter <math> \kappa </math> may vary in <math> \Omega </math>. | The parameter <math> \kappa </math> may vary in <math> \Omega </math>. | ||
Revision as of 16:29, 23 February 2016
| Control of Heat Equation with Actuator Placement | |
|---|---|
| State dimension: | 1 |
| Differential states: | 1 |
| Continuous control functions: |
 |
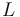| Discrete control functions: |
|
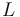| Path constraints: | 3 |
| Interior point equalities: | 2 |
This problem is governed by the heat equation and is adapted from Iftime and Demetriou ([Iftime2009]Author: Orest V. Iftime; Michael A. Demetriou
Journal: {A}utomatica
Number: 2
Pages: 312--323
Title: {O}ptimal control of switched distributed parameter systems with spatially scheduled actuators
Volume: 45
Year: 2009
).
Its goal is to choose a place to apply an actuator in a given area depending on time.
We consider a rectangle ![\Omega=[0,1]\times[0,2]](https://mintoc.de/images/math/b/9/e/b9e9ecbd1ca99669f6d13a62bcf6142b.png)
with the boundary 
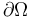and the time horizon ![T=[0,10]](https://mintoc.de/images/math/0/a/e/0aef63dc3199780b7093eeb4bd8d74f5.png)
as the domains.
The objective function is quadratic, its first term captures the desired final state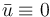 
, the second term regularize the state over time and the third term regularize the continuous controls.
The constraints are a source budget, which limits the quantity of placed actuators, and the two-dimensional heat equation with some source function.
Additionally, we assume Dirichlet boundary conditions and initial conditions.
Mathematical formulation
![\begin{array}{llcl}
\min\limits_{u,v,w}~~ &J(u,v)=||u(\cdot,\cdot,10)||_{2,\Omega}^2 +2||u(\cdot,\cdot,\cdot)||_{2,\Omega\times T}^2+\frac{1}{500}\sum\limits_{l=1}^L||v_l(\cdot)||^2_{2,T} & \\[10pt]
\text{ s.t.} ~~~~ &\frac{\partial u}{\partial t}(x,y,t)- \kappa \Delta u(x,y,t)=\sum\limits_{l=1}^9 v_l(t) f_l(x,y) &\text{ in }&\Omega\times T\\[10pt]
& u(x,y,t) =0 &\text{ on } &\partial\Omega\times T \\[10pt]
& u(x,y,0) = 100 \sin(\pi x)\sin(\pi y) &\text{ in }& \Omega\\[10pt]
& -M w_l(t)\leq v_l(t)\leq M w_l(t) \text{ for all } l\in \{1,\dots,L\} &\text{ in } & T \\[10pt]
& \sum\limits_{l=1}^L w_l(t) = 1 &\text{ in } & T\\[10pt]
& w_l(t)\in \{0,1\} \text{ for all } l\in \{1,\dots,L\} &\text{ in } &T.
\end{array}](https://mintoc.de/images/math/1/6/8/168b422f1c8bd993901de51eac922c9d.png)
Parameters
These fixed values are used within the model.
\\
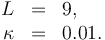The parameter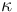 
may vary in 
.
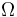Reference solution
Source Code
References
| [Iftime2009] | Orest V. Iftime; Michael A. Demetriou (2009): {O}ptimal control of switched distributed parameter systems with spatially scheduled actuators . {A}utomatica, 45, 312--323 | |
