Difference between revisions of "Control of Heat Equation with Actuator Placement"
FelixMueller (Talk | contribs) (→Parameters) |
FelixMueller (Talk | contribs) (→Parameters) |
||
| Line 39: | Line 39: | ||
| − | + | We define the source term for all locations <math> | |
| + | l\in \{1,\dots,L\} <\math> and a | ||
| + | fix parameter <math>\varepsilon\in \R_+</math>: | ||
| + | <math> | ||
| + | f_l(x,y) = \frac{1}{\sqrt{2\pi\varepsilon}}e^{\frac{-((x_l-x)^2+(y_l-y)^2)}{2\varepsilon}} | ||
| + | <\math> | ||
| + | where <math>(x_l,y_l)</math> is the coordinate of the mesh point of the $l$th possible actuator location. | ||
| + | |||
| + | The parameters used are: | ||
<math> | <math> | ||
| Line 52: | Line 60: | ||
| − | The parameter <math> \kappa </math> describes the thermal dissipativity of the material in the domain <math> \Omega </math>, it may vary in space. | + | The parameter <math> \kappa </math> describes the thermal dissipativity of the material in the domain <math> \Omega </math>, it may vary in space: <math> \kappa(x,y) </math>. |
The parameter <math> L </math> indicates the number of possible actuator locations. They are distributed as indicated in the picture. | The parameter <math> L </math> indicates the number of possible actuator locations. They are distributed as indicated in the picture. | ||
| − | + | The source budget is limited by <math>W<\math>. | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | <\math> | + | |
| − | + | ||
==Reference solution== | ==Reference solution== | ||
Revision as of 18:08, 23 February 2016
| Control of Heat Equation with Actuator Placement | |
|---|---|
| State dimension: | 1 |
| Differential states: | 1 |
| Continuous control functions: |
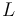 |
| Discrete control functions: |
 |
| Path constraints: | 3 |
| Interior point equalities: | 2 |
This problem is governed by the heat equation and is adapted from Iftime and Demetriou ([Iftime2009]Author: Orest V. Iftime; Michael A. Demetriou
Journal: {A}utomatica
Number: 2
Pages: 312--323
Title: {O}ptimal control of switched distributed parameter systems with spatially scheduled actuators
Volume: 45
Year: 2009 ).
Its goal is to choose a place to apply an actuator in a given area depending on time.
The objective function is quadratic, its first term captures the desired final state
).
Its goal is to choose a place to apply an actuator in a given area depending on time.
The objective function is quadratic, its first term captures the desired final state 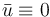 , the second term regularize the state over time and the third term regularize the continuous controls.
The constraints are a source budget, which limits the quantity of placed actuators, and the two-dimensional heat equation with some source function.
Additionally, we assume Dirichlet boundary conditions and initial conditions.
, the second term regularize the state over time and the third term regularize the continuous controls.
The constraints are a source budget, which limits the quantity of placed actuators, and the two-dimensional heat equation with some source function.
Additionally, we assume Dirichlet boundary conditions and initial conditions.
Mathematical formulation
![\begin{array}{llcl}
\min\limits_{u,v,w}~~ &J(u,v)=||u(\cdot,\cdot,t_f)||_{2,\Omega}^2 +2||u(\cdot,\cdot,\cdot)||_{2,\Omega\times T}^2+\frac{1}{500}\sum\limits_{l=1}^L||v_l(\cdot)||^2_{2,T} & \\[10pt]
\text{ s.t.} ~~~~ &\frac{\partial u}{\partial t}(x,y,t)- \kappa \Delta u(x,y,t)=\sum\limits_{l=1}^9 v_l(t) f_l(x,y) &\text{ in }&\Omega\times T\\[10pt]
& u(x,y,t) =0 &\text{ on } &\partial\Omega\times T \\[10pt]
& u(x,y,0) = 100 \sin(\pi x)\sin(\pi y) &\text{ in }& \Omega\\[10pt]
& -M w_l(t)\leq v_l(t)\leq M w_l(t) \text{ for all } l\in \{1,\dots,L\} &\text{ in } & T \\[10pt]
& \sum\limits_{l=1}^L w_l(t) = W &\text{ in } & T\\[10pt]
& w_l(t)\in \{0,1\} \text{ for all } l\in \{1,\dots,L\} &\text{ in } &T.
\end{array}](https://mintoc.de/images/math/7/f/5/7f5aedcd98c25fda943e906977164eee.png)
Parameters
We define the source term for all locations Failed to parse (unknown function "\math"): l\in \{1,\dots,L\} <\math> and a fix parameter <math>\varepsilon\in \R_+
Failed to parse (unknown function "\math"): f_l(x,y) = \frac{1}{\sqrt{2\pi\varepsilon}}e^{\frac{-((x_l-x)^2+(y_l-y)^2)}{2\varepsilon}} <\math> where <math>(x_l,y_l)
is the coordinate of the mesh point of the $l$th possible actuator location.
The parameters used are:
![\begin{array}{rcl}
\Omega &=& [0,1] \times [0,2],\\
L &=& 9, \\
\kappa &=& 0.01,\\
t_f &=&10,\\
W &=& 1.
\end{array}](https://mintoc.de/images/math/9/8/8/988392d33cda2840efd3740fb3daf6b1.png)
The parameter 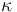 describes the thermal dissipativity of the material in the domain
describes the thermal dissipativity of the material in the domain 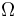 , it may vary in space:
, it may vary in space: 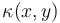 .
The parameter
.
The parameter 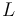 indicates the number of possible actuator locations. They are distributed as indicated in the picture.
The source budget is limited by Failed to parse (unknown function "\math"): W<\math>. ==Reference solution== ==Source Code== ==References== <biblist/> <!--List of all categories this page is part of. List characterization of solution behavior, model properties, ore presence of implementation details (e.g., AMPL for AMPL model) here --> [[Category:MIOCP]]
indicates the number of possible actuator locations. They are distributed as indicated in the picture.
The source budget is limited by Failed to parse (unknown function "\math"): W<\math>. ==Reference solution== ==Source Code== ==References== <biblist/> <!--List of all categories this page is part of. List characterization of solution behavior, model properties, ore presence of implementation details (e.g., AMPL for AMPL model) here --> [[Category:MIOCP]]