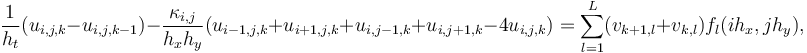Difference between revisions of "Control of Heat Equation with Actuator Placement"
FelixMueller (Talk | contribs) (→Mathematical formulation) |
FelixMueller (Talk | contribs) (→Discretization) |
||
| Line 68: | Line 68: | ||
The source budget is limited by <math>W</math> and <math>t_f</math> denotes the final time. | The source budget is limited by <math>W</math> and <math>t_f</math> denotes the final time. | ||
| − | ==Discretization== | + | <nowiki>Insert non-formatted text here</nowiki>==Discretization== |
To solve the problem we apply a "first discretize, then optimize" approach an discretize the components of the problem. | To solve the problem we apply a "first discretize, then optimize" approach an discretize the components of the problem. | ||
For the heat equation, we use a five-point-stencil in space and the implicit euler in time. | For the heat equation, we use a five-point-stencil in space and the implicit euler in time. | ||
For <math>i=1,\dots, N-1</math>, <math>j=1,\dots, M-1</math>, and <math>k=0,\dots, T_n-1</math>, this yields: | For <math>i=1,\dots, N-1</math>, <math>j=1,\dots, M-1</math>, and <math>k=0,\dots, T_n-1</math>, this yields: | ||
| − | <math> \frac{1}{h_t}(u_{i,j,k}-u_{i,j,k-1}) - \frac{\kappa_{i,j}}{h_x h_y}(u_{i-1,j,k}+u_{i+1,j,k}+u_{i,j-1,k}+u_{i,j+1,k}-4u_{i,j,k}) = \sum\limits_{l=1}^L( | + | <math> \frac{1}{h_t}(u_{i,j,k}-u_{i,j,k-1}) - \frac{\kappa_{i,j}}{h_x h_y}(u_{i-1,j,k}+u_{i+1,j,k}+u_{i,j-1,k}+u_{i,j+1,k}-4u_{i,j,k}) = \sum\limits_{l=1}^L(v_{k+1,l}+v_{k ,l} )f_l(ih_x,jh_y), </math> |
with <math>u_{i,j,k}=u(ih_x,jh_y,kh_t)</math>, the stepsizes <math>h_x,h_y</math> in space, and the stepsize in time <math>h_t</math>, respectively. | with <math>u_{i,j,k}=u(ih_x,jh_y,kh_t)</math>, the stepsizes <math>h_x,h_y</math> in space, and the stepsize in time <math>h_t</math>, respectively. | ||
Revision as of 19:20, 23 February 2016
| Control of Heat Equation with Actuator Placement | |
|---|---|
| State dimension: | 1 |
| Differential states: | 1 |
| Continuous control functions: | 9 |
| Discrete control functions: | 9 |
| Path constraints: | 3 |
| Interior point equalities: | 2 |
This problem is governed by the heat equation and is adapted from Iftime and Demetriou ([Iftime2009]Author: Orest V. Iftime; Michael A. Demetriou
Journal: {A}utomatica
Number: 2
Pages: 312--323
Title: {O}ptimal control of switched distributed parameter systems with spatially scheduled actuators
Volume: 45
Year: 2009 ).
Its goal is to choose a place to apply an actuator in a given area depending on time.
The objective function is quadratic, its first term captures the desired final state
).
Its goal is to choose a place to apply an actuator in a given area depending on time.
The objective function is quadratic, its first term captures the desired final state  , the second term regularize the state over time and the third term regularize the continuous controls.
The constraints are a source budget, which limits the quantity of placed actuators, and the two-dimensional heat equation with some source function.
Additionally, we assume Dirichlet boundary conditions and initial conditions.
Originally, the problem formulation was non-convex.
We overcome this issue by substitution of
, the second term regularize the state over time and the third term regularize the continuous controls.
The constraints are a source budget, which limits the quantity of placed actuators, and the two-dimensional heat equation with some source function.
Additionally, we assume Dirichlet boundary conditions and initial conditions.
Originally, the problem formulation was non-convex.
We overcome this issue by substitution of  by
by  and adding the Big
and adding the Big 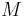 formulation.
formulation.
Mathematical formulation
![\begin{array}{llcl}
\min\limits_{u,v,w}~~ &J(u,v)=||u(\cdot,\cdot,t_f)||_{2,\Omega}^2 +2||u(\cdot,\cdot,\cdot)||_{2,\Omega\times T}^2+\frac{1}{500}\sum\limits_{l=1}^L||v_l(\cdot)||^2_{2,T} & \\[10pt]
\text{ s.t.} ~~~~ &\frac{\partial u}{\partial t}(x,y,t)- \kappa \Delta u(x,y,t)=\sum\limits_{l=1}^9 v_l(t) f_l(x,y) &\text{ in }&\Omega\times T\\[10pt]
& u(x,y,t) =0 &\text{ on } &\partial\Omega\times T \\[10pt]
& u(x,y,0) = 100 \sin(\pi x)\sin(\pi y) &\text{ in }& \Omega\\[10pt]
& -M w_l(t)\leq v_l(t)\leq M w_l(t) \text{ for all } l\in \{1,\dots,L\} &\text{ in } & T \\[10pt]
& \sum\limits_{l=1}^L w_l(t) \leq W &\text{ in } & T\\[10pt]
& w_l(t)\in \{0,1\} \text{ for all } l\in \{1,\dots,L\} &\text{ in } &T.
\end{array}](https://mintoc.de/images/math/1/6/e/16ec5050696389c908c29d1db9257d7c.png)
Parameters
We define the source term for all locations 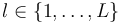 and a
fix parameter
and a
fix parameter 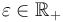 :
:
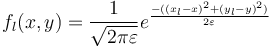 where
where 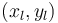 is the coordinate of the mesh point of the
is the coordinate of the mesh point of the 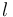 th possible actuator location.
th possible actuator location.
The parameters used are:
![\begin{array}{rcl}
\Omega &=& [0,1] \times [0,2],\\
\kappa &=& 0.01,\\
L &=& 9, \\
W &=& 1,\\
t_f &=&10,\\
\varepsilon &=& 0.01 .
\end{array}](https://mintoc.de/images/math/6/4/5/645059149717567c0c993822f7ba8a87.png)
The parameter 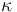 describes the thermal dissipativity of the material in the domain
describes the thermal dissipativity of the material in the domain 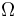 , it may vary in space:
, it may vary in space: 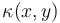 .
The parameter
.
The parameter 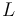 indicates the number of possible actuator locations. They are distributed as indicated in the picture.
The source budget is limited by
indicates the number of possible actuator locations. They are distributed as indicated in the picture.
The source budget is limited by 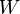 and
and 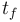 denotes the final time.
denotes the final time.
Insert non-formatted text here==Discretization==
To solve the problem we apply a "first discretize, then optimize" approach an discretize the components of the problem.
For the heat equation, we use a five-point-stencil in space and the implicit euler in time.
For 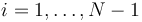 ,
,  , and
, and  , this yields:
, this yields:
with 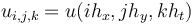 , the stepsizes
, the stepsizes 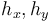 in space, and the stepsize in time
in space, and the stepsize in time 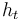 , respectively.
, respectively.
It holds for the source buget with the discretized binary controls 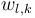 for all
for all 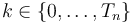 :
:
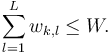
This condition is called SOS- conditon.
conditon.
We remark that the number of discretized binary variables does not depend on the space discretization but it depends on the time discretization. Thats why we taged this problem containing mesh-independend and as mesh-dependend integer variables.
Source Code
References
| [Iftime2009] | Orest V. Iftime; Michael A. Demetriou (2009): {O}ptimal control of switched distributed parameter systems with spatially scheduled actuators . {A}utomatica, 45, 312--323 |  |