Difference between revisions of "Lotka Volterra fishing problem (APMonitor)"

From mintOC
Jump to: navigation, search
(APMontor solution of Volterra fishing problem)
 
(Results section)
Line 107: Line 107:
 
</source>
 
</source>
  
−
== Results ==
+
== Results with APOPT (MINLP) ==
  
−
=== IPOPT ===
+
An MINLP solution is calculated with [https://apopt.com|APOPT] with an objective function value of <math>x_2(t_f) = 1.36</math>. APOPT requires 52 NLP solutions to find an integer solution (111.0 seconds of processing time).
−
The relaxed solution calculated by IPOPT (Ipopt 3.12, Linux x86_64, default settings, 4 GHz quadcore, Linux 4.2.0-23-generic) has an objective function value of <math>x_2(t_f) = 1.34428</math>. IPOPT requires 22 iterations (6.062 seconds of processing time). The following is a Gnuplot compatible tabular version of the solution:
+
 
 +
[[File:Volterra_fishing_APMonitor.png]]
  
 
<pre>
 
<pre>
−
#        t,        x_0,        x_1,          u
+
----------------------------------------------------------------
−
          0,         0.5,        0.7, 5.18436e-09
+
APMonitor, Version 0.7.9
−
      0.12,   0.519594,   0.659989, 5.42459e-09
+
APMonitor Optimization Suite
−
      0.24,   0.542429,   0.623852, 5.79496e-09
+
----------------------------------------------------------------
−
      0.36,   0.568601,   0.591429, 6.30563e-09
+
−
      0.48,    0.59823,   0.562571, 6.97415e-09
+
−
        0.6,   0.631456,   0.537143,  7.827e-09
+
--------- APM Model Size ------------
−
      0.72,    0.66843,    0.515028, 8.90236e-09
+
Each time step contains
−
      0.84,    0.709312,    0.496134, 1.02545e-08
+
   Objects      :            0
−
      0.96,     0.75426,   0.480401, 1.19611e-08
+
   Constants    :            2
−
      1.08,    0.803421,     0.4678, 1.41346e-08
+
   Variables   :            5
−
        1.2,    0.856919,   0.458344, 1.69417e-08
+
   Intermediates:            1
−
      1.32,    0.914842,    0.452091, 2.06377e-08
+
   Connections  :            0
−
      1.44,     0.97722,   0.449154, 2.56285e-08
+
   Equations    :            5
−
      1.56,       1.044,    0.449708, 3.2592e-08
+
   Residuals   :            4
−
      1.68,     1.11503,   0.454003, 4.27322e-08
+
−
        1.8,     1.18998,   0.462372, 5.83658e-08
+
Number of state variables:          2178
−
      1.92,    1.26837,   0.475251, 8.44574e-08
+
Number of total equations: -         2057
−
      2.04,    1.34942,    0.493189, 1.33425e-07
+
Number of slack variables: -            0
−
      2.16,     1.43209,    0.516862, 2.44977e-07
+
---------------------------------------
−
      2.28,    1.51492,   0.547087, 6.24464e-07
+
Degrees of freedom      :            121
−
        2.4,     1.59605,   0.584816,   0.715281
+
−
      2.52,     1.61776,     0.61833,   0.999999
+
----------------------------------------------
−
      2.64,    1.61116,      0.6499,   0.999999
+
Dynamic Control with APOPT Solver
−
      2.76,    1.59844,    0.68229,          1
+
----------------------------------------------
−
      2.88,    1.57963,   0.714939,          1
+
Iter:     1 I:  0 Tm:    12.99 NLPi:  93 Dpth:   0 Lvs:    2 Obj:  1.34E+00 Gap:      NaN
−
          3,    1.55497,   0.747196,          1
+
Iter:    2 I:  0 Tm:     2.82 NLPi:  18 Dpth:   1 Lvs:    3 Obj:  1.34E+00 Gap:      NaN
−
      3.12,    1.52487,   0.778343,    0.999999
+
Iter:     3 I:  0 Tm:      3.39 NLPi:  30 Dpth:   2 Lvs:    4 Obj:  1.34E+00 Gap:       NaN
−
      3.24,    1.48993,   0.807625,    0.999999
+
Iter:    4 I:  0 Tm:    10.37 NLPi: 131 Dpth:    3 Lvs:    5 Obj:  1.34E+00 Gap:      NaN
−
      3.36,      1.4509,    0.83429,   0.999999
+
Iter:     5 I:  0 Tm:      1.81 NLPi:  10 Dpth:   4 Lvs:    6 Obj:  1.34E+00 Gap:      NaN
−
      3.48,    1.40865,   0.857635,    0.999998
+
Iter:     6 I:  0 Tm:      7.93 NLPi:  102 Dpth:   5 Lvs:   7 Obj:  1.34E+00 Gap:      NaN
−
        3.6,    1.36412,   0.877047,    0.999997
+
Iter:     7 I:  0 Tm:      3.22 NLPi:  28 Dpth:   6 Lvs:    8 Obj:  1.34E+00 Gap:      NaN
−
      3.72,    1.31827,   0.892039,    0.999991
+
Iter:     8 I:  0 Tm:      1.85 NLPi:  12 Dpth:   7 Lvs:   9 Obj:  1.34E+00 Gap:      NaN
−
      3.84,    1.27203,    0.90228,   0.999646
+
Iter:     9 I:  0 Tm:     10.24 NLPi:  140 Dpth:   8 Lvs:  10 Obj:  1.34E+00 Gap:      NaN
−
      3.96,    1.22628,   0.907616,   0.536112
+
Iter:   10 I:  0 Tm:      2.04 NLPi:    9 Dpth:    9 Lvs:  11 Obj:  1.35E+00 Gap:      NaN
−
      4.08,    1.20755,   0.919653,   0.581667
+
Iter:   11 I:  0 Tm:      6.50 NLPi:  86 Dpth:  10 Lvs:  12 Obj:  1.35E+00 Gap:      NaN
−
        4.2,    1.18502,   0.928525,    0.503883
+
Iter:   12 I:  0 Tm:      1.94 NLPi:  17 Dpth:  11 Lvs:  13 Obj:  1.35E+00 Gap:      NaN
−
      4.32,    1.16606,   0.936899,    0.464153
+
Iter:   13 I:  0 Tm:      2.17 NLPi:  18 Dpth:  12 Lvs:  14 Obj:  1.35E+00 Gap:      NaN
−
      4.44,    1.14851,   0.944178,   0.418428
+
Iter:   14 I:  0 Tm:      3.56 NLPi:  44 Dpth:  13 Lvs:  15 Obj:  1.35E+00 Gap:      NaN
−
      4.56,    1.13278,   0.950658,    0.378617
+
Iter:   15 I:  0 Tm:      2.34 NLPi:  23 Dpth:  14 Lvs:  16 Obj:  1.35E+00 Gap:      NaN
−
      4.68,    1.11859,   0.956378,   0.341493
+
Iter:   16 I:  0 Tm:      2.46 NLPi:  26 Dpth:  15 Lvs:  17 Obj:  1.35E+00 Gap:      NaN
−
        4.8,    1.10582,   0.961433,     0.3073
+
Iter:   17 I:  0 Tm:      2.72 NLPi:  26 Dpth:  16 Lvs:  18 Obj:  1.35E+00 Gap:      NaN
−
      4.92,    1.09438,   0.965904,   0.276462
+
Iter:   18 I:  0 Tm:      3.99 NLPi:  60 Dpth:  17 Lvs:  19 Obj:  1.35E+00 Gap:      NaN
−
      5.04,    1.08411,   0.969849,    0.248219
+
Iter:   19 I:  0 Tm:      1.91 NLPi:  10 Dpth:  18 Lvs:  20 Obj:  1.35E+00 Gap:      NaN
−
      5.16,    1.07492,   0.973333,    0.222481
+
Iter:   20 I:  0 Tm:      1.23 NLPi:   7 Dpth:  19 Lvs:  21 Obj:  1.35E+00 Gap:      NaN
−
      5.28,      1.0667,   0.976412,    0.19935
+
Iter:   21 I:  0 Tm:      1.37 NLPi:   8 Dpth:  20 Lvs:  22 Obj:  1.35E+00 Gap:      NaN
−
        5.4,    1.05936,    0.97913,   0.178262
+
Iter:   22 I:  0 Tm:      1.37 NLPi:  12 Dpth:  21 Lvs:  23 Obj:  1.35E+00 Gap:      NaN
−
      5.52,     1.0528,    0.981533,   0.159402
+
Iter:   23 I:  0 Tm:      1.34 NLPi:  11 Dpth:  22 Lvs:  24 Obj:  1.36E+00 Gap:      NaN
−
      5.64,    1.04696,   0.983656,   0.142349
+
Iter:   24 I:  0 Tm:      1.30 NLPi:   8 Dpth:  23 Lvs:  25 Obj:  1.36E+00 Gap:      NaN
−
      5.76,    1.04175,   0.985532,   0.127041
+
Iter:   25 I:  0 Tm:      1.33 NLPi:  14 Dpth:  24 Lvs:  26 Obj:  1.36E+00 Gap:      NaN
−
      5.88,      1.0371,   0.987191,     0.1133
+
Iter:   26 I:  0 Tm:      1.13 NLPi:   7 Dpth:  25 Lvs:  27 Obj:  1.36E+00 Gap:      NaN
−
          6,    1.03297,    0.988657,    0.100985
+
Iter:   27 I:  0 Tm:     0.97 NLPi:    7 Dpth:  26 Lvs:  28 Obj:  1.36E+00 Gap:      NaN
−
      6.12,    1.02929,   0.989954,  0.0899604
+
Iter:   28 I:  0 Tm:      0.99 NLPi:   6 Dpth:  27 Lvs:  29 Obj:  1.36E+00 Gap:      NaN
−
      6.24,    1.02601,   0.991101,   0.0800981
+
Iter:   29 I:  0 Tm:      0.93 NLPi:   6 Dpth:  28 Lvs:  30 Obj:  1.36E+00 Gap:      NaN
−
      6.36,      1.0231,   0.992117,  0.0712934
+
Iter:   30 I:  0 Tm:      0.66 NLPi:    5 Dpth:  29 Lvs:  31 Obj:  1.36E+00 Gap:      NaN
−
      6.48,    1.02051,   0.993015,   0.0634308
+
Iter:   31 I:  0 Tm:     0.73 NLPi:   5 Dpth:  30 Lvs:  32 Obj:  1.36E+00 Gap:      NaN
−
        6.6,    1.01821,   0.993811,  0.0564127
+
Iter:   32 I:  0 Tm:      0.66 NLPi:   5 Dpth:  31 Lvs:  33 Obj:  1.36E+00 Gap:      NaN
−
      6.72,    1.01617,   0.994515,   0.0501573
+
Iter:   33 I:  0 Tm:      0.70 NLPi:   5 Dpth:  32 Lvs:  34 Obj:  1.36E+00 Gap:      NaN
−
      6.84,    1.01435,   0.995139,  0.0445824
+
Iter:   34 I:  0 Tm:     0.67 NLPi:    5 Dpth:  33 Lvs:  35 Obj:  1.36E+00 Gap:      NaN
−
      6.96,    1.01274,    0.995691,   0.0396177
+
Iter:   35 I:  0 Tm:      0.82 NLPi:   9 Dpth:  34 Lvs:   36 Obj:  1.36E+00 Gap:      NaN
−
      7.08,    1.01131,    0.99618,  0.0351979
+
Iter:   36 I:  0 Tm:      0.77 NLPi:   8 Dpth:  35 Lvs:   37 Obj:  1.36E+00 Gap:      NaN
−
        7.2,    1.01003,   0.996613,  0.0312714
+
Iter:   37 I:  0 Tm:      0.75 NLPi:   8 Dpth:   36 Lvs:  38 Obj:  1.36E+00 Gap:      NaN
−
      7.32,     1.0089,    0.996997,   0.027765
+
Iter:   38 I:  0 Tm:      0.69 NLPi:    6 Dpth:   37 Lvs:  39 Obj:  1.36E+00 Gap:      NaN
−
      7.44,      1.0079,   0.997337,  0.0246626
+
Iter:   39 I:  0 Tm:     0.71 NLPi:   6 Dpth:  38 Lvs:  40 Obj:  1.36E+00 Gap:      NaN
−
      7.56,    1.00701,   0.997639,   0.0218975
+
Iter:   40 I:  0 Tm:      0.81 NLPi:   9 Dpth:   39 Lvs:  41 Obj:  1.36E+00 Gap:      NaN
−
      7.68,    1.00622,   0.997905,  0.0194423
+
Iter:   41 I:  0 Tm:      0.70 NLPi:    8 Dpth:  40 Lvs:  42 Obj:  1.36E+00 Gap:      NaN
−
        7.8,    1.00552,   0.998142,  0.0172603
+
Iter:   42 I:  0 Tm:      0.69 NLPi:   6 Dpth:   41 Lvs:  43 Obj:  1.36E+00 Gap:      NaN
−
      7.92,      1.0049,   0.998351,   0.0153224
+
Iter:   43 I:  0 Tm:      0.67 NLPi:   5 Dpth:  42 Lvs:   44 Obj:  1.36E+00 Gap:      NaN
−
      8.04,    1.00435,   0.998537,  0.0136015
+
Iter:   44 I:  0 Tm:      0.60 NLPi:    4 Dpth:  43 Lvs:  45 Obj:  1.36E+00 Gap:      NaN
−
      8.16,    1.00386,   0.998701,   0.0120735
+
Iter:   45 I: 0 Tm:      0.71 NLPi:    6 Dpth:  44 Lvs:  46 Obj: 1.36E+00 Gap:      NaN
−
      8.28,    1.00342,   0.998847,  0.0107171
+
Iter:   46 I: 0 Tm:      0.59 NLPi:    4 Dpth:  45 Lvs:  47 Obj: 1.36E+00 Gap:      NaN
−
        8.4,    1.00303,   0.998976, 0.00951328
+
Iter:   47 I: 0 Tm:      0.69 NLPi:   6 Dpth:  46 Lvs:  48 Obj: 1.36E+00 Gap:      NaN
−
      8.52,    1.00269,    0.99909, 0.00844491
+
Iter:   48 I: 0 Tm:      0.65 NLPi:   5 Dpth:  47 Lvs:  49 Obj: 1.36E+00 Gap:      NaN
−
      8.64,    1.00239,    0.999191,  0.00749702
+
--Integer Solution:  1.36E+00 Lowest Leaf:  1.34E+00 Gap:  1.35E-02
−
      8.76,    1.00212,   0.999281, 0.00665598
+
Iter:   49 I: 0 Tm:      0.57 NLPi:   3 Dpth:  48 Lvs:  48 Obj: 1.36E+00 Gap: 1.35E-02
−
      8.88,    1.00188,    0.99936, 0.00590975
+
Iter:   50 I: 0 Tm:      1.29 NLPi:   8 Dpth:  48 Lvs:  47 Obj: 1.36E+00 Gap: 1.35E-02
−
          9,    1.00167,    0.99943,  0.00524776
+
  Warning: best integer solution returned after maximum MINLP iterations
−
      9.12,    1.00148,   0.999492, 0.00466052
+
  Adjust minlp_max_iter_with_int_sol          50  in apopt.opt to change limit
−
      9.24,    1.00131,   0.999547, 0.00413914
+
  Successful solution
−
      9.36,    1.00117,   0.999596, 0.00367206
+
−
      9.48,    1.00103,   0.999637, 0.00326159
+
  ---------------------------------------------------
−
        9.6,    1.00092,    0.999675,  0.00290302
+
Solver        :  APOPT (v1.0)
−
      9.72,    1.00082,   0.999707, 0.00258504
+
Solution time  :   111.364099999999      sec
−
      9.84,    1.00072,   0.999736, 0.00230262
+
Objective      :   1.36258198934523      
−
      9.96,    1.00064,    0.999762, 0.00205186
+
  Successful solution
−
      10.08,    1.00057,   0.999785, 0.00182951
+
  ---------------------------------------------------
−
      10.2,    1.00051,   0.999805, 0.00163302
+
−
      10.32,    1.00045,    0.999822, 0.00146039
+
−
      10.44,      1.0004,    0.999838, 0.00131011
+
−
      10.56,    1.00036,    0.999851, 0.00118097
+
−
      10.68,    1.00032,    0.999863, 0.00107188
+
−
      10.8,    1.00028,    0.999872, 0.000981659
+
−
      10.92,    1.00025,    0.99988, 0.00090944
+
−
      11.04,    1.00022,    0.999886, 0.000854893
+
−
      11.16,    1.00019,    0.99989, 0.000818284
+
−
      11.28,    1.00017,   0.999892, 0.000801181
+
−
      11.4,    1.00014,   0.999891, 0.000807844
+
−
      11.52,    1.00012,    0.999886, 0.000848734
+
−
      11.64,     1.00009,    0.999878, 0.000951928
+
−
      11.76,    1.00006,    0.999864, 0.00121852
+
−
      11.88,    1.00002,    0.999838, 0.00267036
+
−
        12,    0.999915,    0.999769,          0
+
 
</pre>
 
</pre>
 +
 +
 
   
 
   
 
[[Category:APMonitor]]
 
[[Category:APMonitor]]

Revision as of 23:12, 20 November 2017

This page contains a solution of the MIOCP Lotka Volterra fishing problem in APMonitor Python format. A MATLAB version is also available from the Dynamic Optimization Course as Example 3 (lotka_volterra_fishing.zip).

APMonitor

The model in Python code for a fixed control discretization grid using orthogonal collocation and a simultaneous optimization method. The APMonitor package is available with pip install APMonitor or from the APMonitor Python Github repository. 

import numpy as np
import matplotlib.pyplot as plt
 
# retrieve apm.py from
# https://raw.githubusercontent.com/APMonitor/apm_python/master/apm.py
# or
# http://apmonitor.com/wiki/index.php/Main/PythonApp
# from apm import *
 
# pip install with 'pip install APMonitor'
from APMonitor.apm import *
 
# local APMonitor servers are available for Windows or Linux
# http://apmonitor.com/wiki/index.php/Main/APMonitorServer
# with clients in Python, MATLAB, and Julia
 
# write model
model = '''
! apopt MINLP solver options (see apopt.com)
File apopt.opt
 minlp_maximum_iterations 1000     ! minlp iterations
 minlp_max_iter_with_int_sol 50    ! minlp iterations if integer solution is found
 minlp_as_nlp 0                    ! treat minlp as nlp
 nlp_maximum_iterations 200        ! nlp sub-problem max iterations
 minlp_branch_method 1             ! 1 = depth first, 2 = breadth first
 minlp_gap_tol 0.001               ! covergence tolerance
 minlp_integer_tol 0.001           ! maximum deviation from whole number to be considered an integer
 minlp_integer_leaves 0            ! create soft (1) integer leaves or hard (2) integer leaves with branching  
End File
 
Constants
  c0 = 0.4 
  c1 = 0.2
 
Parameters
  last
 
Variables
  x0 = 0.5 , >= 0
  x1 = 0.7 , >= 0
  x2 = 0.0 , >= 0
  int_w = 0 , >= 0 , <= 1
 
Intermediates
  w = int_w
 
Equations
  minimize last * x2
 
  $x0 = x0 - x0*x1 - c0*x0*w 
  $x1 = - x1 + x0*x1 - c1*x1*w
  $x2 = (x0-1)^2 + (x1-1)^2                                                                                       
'''
fid = open('lotka_volterra.apm','w')
fid.write(model)
fid.close()
 
# write data file
time = np.linspace(0,12,121)
time = np.insert(time, 1, 0.01)
last = np.zeros(122)
last[-1] = 1.0
data = np.vstack((time,last))
np.savetxt('data.csv',data.T,delimiter=',',header='time,last',comments='')
 
# specify server and application name
s = 'http://byu.apmonitor.com'
#s = 'http://127.0.0.1/'  # for local APMonitor server
a = 'lotka'
 
apm(s,a,'clear all')
apm_load(s,a,'lotka_volterra.apm')
csv_load(s,a,'data.csv')
 
apm_option(s,a,'nlc.imode',6)              # Nonlinear control / dynamic optimization
apm_option(s,a,'nlc.nodes',3)
 
apm_info(s,a,'MV','int_w')                 # M or MV = Manipulated variable - independent variable over time horizon
apm_option(s,a,'int_w.status',1)           # Status: 1=ON, 0=OFF
apm_option(s,a,'int_w.mv_type',0)          # MV Type = Zero Order Hold
 
apm_option(s,a,'nlc.solver',1)             # 1 = APOPT
 
# solve
output = apm(s,a,'solve')            
print(output)
 
# retrieve solution
y = apm_sol(s,a)
 
plt.figure(1)
plt.step(y['time'],y['int_w'],'r-',label='w (0/1)')
plt.plot(y['time'],y['x0'],'b-',label=r'$x_0$')
plt.plot(y['time'],y['x1'],'k-',label=r'$x_1$')
plt.plot(y['time'],y['x2'],'g-',label=r'$x_2$')
plt.xlabel('Time')
plt.ylabel('Variables')
plt.legend(loc='best')
plt.show()

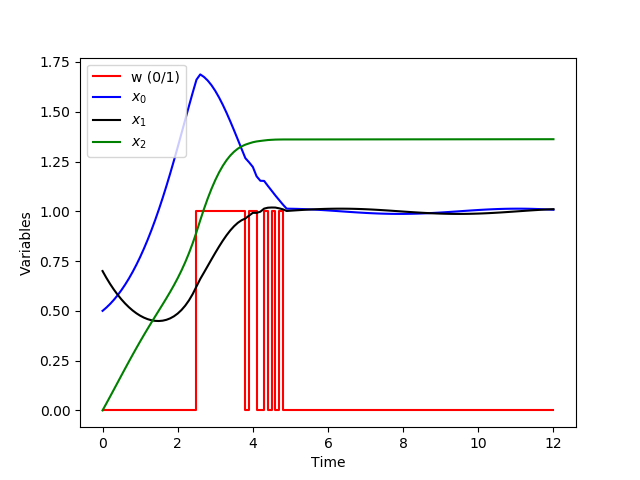
Results with APOPT (MINLP)

An MINLP solution is calculated with [1] with an objective function value of 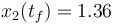x_2(t_f) = 1.36. APOPT requires 52 NLP solutions to find an integer solution (111.0 seconds of processing time).

Volterra fishing APMonitor.png 

 ----------------------------------------------------------------
 APMonitor, Version 0.7.9
 APMonitor Optimization Suite
 ----------------------------------------------------------------
 
 
 --------- APM Model Size ------------
 Each time step contains
   Objects      :            0
   Constants    :            2
   Variables    :            5
   Intermediates:            1
   Connections  :            0
   Equations    :            5
   Residuals    :            4
 
 Number of state variables:           2178
 Number of total equations: -         2057
 Number of slack variables: -            0
 ---------------------------------------
 Degrees of freedom       :            121
 
 ----------------------------------------------
 Dynamic Control with APOPT Solver
 ----------------------------------------------
Iter:     1 I:  0 Tm:     12.99 NLPi:   93 Dpth:    0 Lvs:    2 Obj:  1.34E+00 Gap:       NaN
Iter:     2 I:  0 Tm:      2.82 NLPi:   18 Dpth:    1 Lvs:    3 Obj:  1.34E+00 Gap:       NaN
Iter:     3 I:  0 Tm:      3.39 NLPi:   30 Dpth:    2 Lvs:    4 Obj:  1.34E+00 Gap:       NaN
Iter:     4 I:  0 Tm:     10.37 NLPi:  131 Dpth:    3 Lvs:    5 Obj:  1.34E+00 Gap:       NaN
Iter:     5 I:  0 Tm:      1.81 NLPi:   10 Dpth:    4 Lvs:    6 Obj:  1.34E+00 Gap:       NaN
Iter:     6 I:  0 Tm:      7.93 NLPi:  102 Dpth:    5 Lvs:    7 Obj:  1.34E+00 Gap:       NaN
Iter:     7 I:  0 Tm:      3.22 NLPi:   28 Dpth:    6 Lvs:    8 Obj:  1.34E+00 Gap:       NaN
Iter:     8 I:  0 Tm:      1.85 NLPi:   12 Dpth:    7 Lvs:    9 Obj:  1.34E+00 Gap:       NaN
Iter:     9 I:  0 Tm:     10.24 NLPi:  140 Dpth:    8 Lvs:   10 Obj:  1.34E+00 Gap:       NaN
Iter:    10 I:  0 Tm:      2.04 NLPi:    9 Dpth:    9 Lvs:   11 Obj:  1.35E+00 Gap:       NaN
Iter:    11 I:  0 Tm:      6.50 NLPi:   86 Dpth:   10 Lvs:   12 Obj:  1.35E+00 Gap:       NaN
Iter:    12 I:  0 Tm:      1.94 NLPi:   17 Dpth:   11 Lvs:   13 Obj:  1.35E+00 Gap:       NaN
Iter:    13 I:  0 Tm:      2.17 NLPi:   18 Dpth:   12 Lvs:   14 Obj:  1.35E+00 Gap:       NaN
Iter:    14 I:  0 Tm:      3.56 NLPi:   44 Dpth:   13 Lvs:   15 Obj:  1.35E+00 Gap:       NaN
Iter:    15 I:  0 Tm:      2.34 NLPi:   23 Dpth:   14 Lvs:   16 Obj:  1.35E+00 Gap:       NaN
Iter:    16 I:  0 Tm:      2.46 NLPi:   26 Dpth:   15 Lvs:   17 Obj:  1.35E+00 Gap:       NaN
Iter:    17 I:  0 Tm:      2.72 NLPi:   26 Dpth:   16 Lvs:   18 Obj:  1.35E+00 Gap:       NaN
Iter:    18 I:  0 Tm:      3.99 NLPi:   60 Dpth:   17 Lvs:   19 Obj:  1.35E+00 Gap:       NaN
Iter:    19 I:  0 Tm:      1.91 NLPi:   10 Dpth:   18 Lvs:   20 Obj:  1.35E+00 Gap:       NaN
Iter:    20 I:  0 Tm:      1.23 NLPi:    7 Dpth:   19 Lvs:   21 Obj:  1.35E+00 Gap:       NaN
Iter:    21 I:  0 Tm:      1.37 NLPi:    8 Dpth:   20 Lvs:   22 Obj:  1.35E+00 Gap:       NaN
Iter:    22 I:  0 Tm:      1.37 NLPi:   12 Dpth:   21 Lvs:   23 Obj:  1.35E+00 Gap:       NaN
Iter:    23 I:  0 Tm:      1.34 NLPi:   11 Dpth:   22 Lvs:   24 Obj:  1.36E+00 Gap:       NaN
Iter:    24 I:  0 Tm:      1.30 NLPi:    8 Dpth:   23 Lvs:   25 Obj:  1.36E+00 Gap:       NaN
Iter:    25 I:  0 Tm:      1.33 NLPi:   14 Dpth:   24 Lvs:   26 Obj:  1.36E+00 Gap:       NaN
Iter:    26 I:  0 Tm:      1.13 NLPi:    7 Dpth:   25 Lvs:   27 Obj:  1.36E+00 Gap:       NaN
Iter:    27 I:  0 Tm:      0.97 NLPi:    7 Dpth:   26 Lvs:   28 Obj:  1.36E+00 Gap:       NaN
Iter:    28 I:  0 Tm:      0.99 NLPi:    6 Dpth:   27 Lvs:   29 Obj:  1.36E+00 Gap:       NaN
Iter:    29 I:  0 Tm:      0.93 NLPi:    6 Dpth:   28 Lvs:   30 Obj:  1.36E+00 Gap:       NaN
Iter:    30 I:  0 Tm:      0.66 NLPi:    5 Dpth:   29 Lvs:   31 Obj:  1.36E+00 Gap:       NaN
Iter:    31 I:  0 Tm:      0.73 NLPi:    5 Dpth:   30 Lvs:   32 Obj:  1.36E+00 Gap:       NaN
Iter:    32 I:  0 Tm:      0.66 NLPi:    5 Dpth:   31 Lvs:   33 Obj:  1.36E+00 Gap:       NaN
Iter:    33 I:  0 Tm:      0.70 NLPi:    5 Dpth:   32 Lvs:   34 Obj:  1.36E+00 Gap:       NaN
Iter:    34 I:  0 Tm:      0.67 NLPi:    5 Dpth:   33 Lvs:   35 Obj:  1.36E+00 Gap:       NaN
Iter:    35 I:  0 Tm:      0.82 NLPi:    9 Dpth:   34 Lvs:   36 Obj:  1.36E+00 Gap:       NaN
Iter:    36 I:  0 Tm:      0.77 NLPi:    8 Dpth:   35 Lvs:   37 Obj:  1.36E+00 Gap:       NaN
Iter:    37 I:  0 Tm:      0.75 NLPi:    8 Dpth:   36 Lvs:   38 Obj:  1.36E+00 Gap:       NaN
Iter:    38 I:  0 Tm:      0.69 NLPi:    6 Dpth:   37 Lvs:   39 Obj:  1.36E+00 Gap:       NaN
Iter:    39 I:  0 Tm:      0.71 NLPi:    6 Dpth:   38 Lvs:   40 Obj:  1.36E+00 Gap:       NaN
Iter:    40 I:  0 Tm:      0.81 NLPi:    9 Dpth:   39 Lvs:   41 Obj:  1.36E+00 Gap:       NaN
Iter:    41 I:  0 Tm:      0.70 NLPi:    8 Dpth:   40 Lvs:   42 Obj:  1.36E+00 Gap:       NaN
Iter:    42 I:  0 Tm:      0.69 NLPi:    6 Dpth:   41 Lvs:   43 Obj:  1.36E+00 Gap:       NaN
Iter:    43 I:  0 Tm:      0.67 NLPi:    5 Dpth:   42 Lvs:   44 Obj:  1.36E+00 Gap:       NaN
Iter:    44 I:  0 Tm:      0.60 NLPi:    4 Dpth:   43 Lvs:   45 Obj:  1.36E+00 Gap:       NaN
Iter:    45 I:  0 Tm:      0.71 NLPi:    6 Dpth:   44 Lvs:   46 Obj:  1.36E+00 Gap:       NaN
Iter:    46 I:  0 Tm:      0.59 NLPi:    4 Dpth:   45 Lvs:   47 Obj:  1.36E+00 Gap:       NaN
Iter:    47 I:  0 Tm:      0.69 NLPi:    6 Dpth:   46 Lvs:   48 Obj:  1.36E+00 Gap:       NaN
Iter:    48 I:  0 Tm:      0.65 NLPi:    5 Dpth:   47 Lvs:   49 Obj:  1.36E+00 Gap:       NaN
--Integer Solution:   1.36E+00 Lowest Leaf:   1.34E+00 Gap:   1.35E-02
Iter:    49 I:  0 Tm:      0.57 NLPi:    3 Dpth:   48 Lvs:   48 Obj:  1.36E+00 Gap:  1.35E-02
Iter:    50 I:  0 Tm:      1.29 NLPi:    8 Dpth:   48 Lvs:   47 Obj:  1.36E+00 Gap:  1.35E-02
 Warning: best integer solution returned after maximum MINLP iterations
 Adjust minlp_max_iter_with_int_sol           50  in apopt.opt to change limit
 Successful solution
 
 ---------------------------------------------------
 Solver         :  APOPT (v1.0)
 Solution time  :    111.364099999999      sec
 Objective      :    1.36258198934523     
 Successful solution
 ---------------------------------------------------
Retrieved from "https://mintoc.de/index.php?title=Lotka_Volterra_fishing_problem_(APMonitor)&oldid=2153"