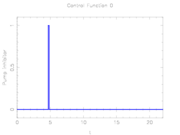
Difference between revisions of "Annihilation of calcium oscillations"

From mintOC
Jump to: navigation, search
m (New page: {{Dimensions |nd = 1 |nx = 4 |nw = 1 |nre = 3 }} The aim of the control problem is to identify strength and timing of inhibitor stimuli that lead to a phase sin...)
(No difference)

Revision as of 14:17, 12 November 2008

Annihilation of calcium oscillations
State dimension: 1
Differential states: 4
Discrete control functions: 1
Interior point equalities: 3


The aim of the control problem is to identify strength and timing of inhibitor stimuli that lead to a phase singularity which annihilates intracellular calcium oscillations. This is formulated as an objective function that aims at minimizing the state deviation from a desired unstable steady state, integrated over time.

Biological rhythms as impressing manifestations of self-organized dynamics associated with the phenomenon life have been of particular interest since quite a long time. Even before the mechanistic basis of certain biochemical oscillators was elucidated by molecular biology techniques, their investigation and the issue of perturbation by external stimuli has attracted much attention.

A calcium oscillator model describing intracellular calcium spiking in hepatocytes induced by an extracellular increase in adenosine triphosphate (ATP) concentration is described. The calcium signaling pathway is initiated via a receptor activated G-protein inducing the intracellular release of inositol triphoshate (IP3) by phospholipase C. The IP3 triggers the opening of endoplasmic reticulum and plasma membrane calcium channels and a subsequent inflow of calcium ions from intracellular and extracellular stores leading to transient calcium spikes.

As a source of external control a temporally varying concentration of an uncompetitive inhibitor of the PMCA ion pump is considered.

The mathematical equations form a small-scale ODE model. The interior point equality conditions fix the initial values of the differential states. The problem is, despite of its low dimension, very hard to solve, as the target state is.

Mathematical formulation

For t \in [t_0, t_f] almost everywhere the mixed-integer optimal control problem is given by

\begin{array}{llcl} \displaystyle \min_{x, w, w^{\mathrm{max}}} & & & {\int_{t_0}^{t_f} || x(\tau) - \tilde{x} ||_2^2 \mathrm{d}\tau} \\[1.5ex] \mbox{s.t.} & \dot{x}_0 & = & k_1 + k_2 x_0 - \frac{k_3 x_0 x_1}{x_0 + K_4} - \frac{k_5 x_0 x_2}{x_0 + K_6} \\ & \dot{x}_1 & = & k_7 x_0 - \frac{k_8 x_1}{x_1 + K_9} \\ & \dot{x}_2 & = & \frac{k_{10} x_1 x_2 x_3}{x_3 + K_{11}} + k_{12} x_1 + k_{13} x_0 - \frac{k_{14} x_2}{{w} x_2 + K_{15}} - \frac{k_{16} x_2}{x_2 + K_{17}} + \frac{x_3}{10} \\ & \dot{x}_3 & = & - \frac{k_{10} x_1 x_2 x_3}{x_3 + K_{11}} + \frac{k_{16} x_2}{x_2 + K_{17}} - \frac{x_3}{10} \\[1.5ex] & x(0) &=& (0.03966, 1.09799, 0.00142, 1.65431)^T, \\ & w(t) &\in& \{0, w^{\mathrm{max}}\}. \end{array}

Here the differential states 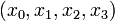(x_0, x_1, x_2, x_3) describe concentrations of activated G-proteins, active phospholipase C, intracellular calcium, and intra-ER calcium, respectively.

Modeling details including a comprehensive discussion of parameter values and the dynamical behavior observed in simulations with a comparison to experimental observations can be found in <bibref>Kummer2000</bibref>. In the given equations that stem from <bibref>Lebiedz2005</bibref>, the model is identical to the one derived there, except for an additional first-order leakage flow of calcium from the ER back to the cytoplasm, which is modeled by 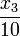\frac{x_3}{10} in equations 3 and 4. It reproduces well experimental observations of cytoplasmic calcium oscillations as well as bursting behavior and in particular the frequency encoding of the triggering stimulus strength, which is a well known mechanism for signal processing in cell biology.

Parameters

These fixed values are used within the model.

\begin{array}{rcl} [t_0, t_f] &=& [0, 22],\\ k_1 &=& 0.09, \\ k_2 &=& 2.30066, \\ k_3 &=& 0.64, \\ K_4 &=& 0.19, \\ k_5 &=& 4.88, \\ K_6 &=& 1.18, \\ k_7 &=& 2.08, \\ k_8 &=& 32.24, \\ K_9 &=& 29.09, \\ k_{10} &=& 5.0, \\ K_{11} &=& 2.67, \\ k_{12} &=& 0.7, \\ k_{13} &=& 13.58, \\ k_{14} &=& 153.0, \\ K_{15} &=& 0.16, \\ k_{16} &=& 4.85, \\ K_{17} &=& 0.05, \\ p_1 &=& 100, \\ p_2 &=& 5. \end{array}

Reference Solutions

  • Reference solution plots

  • Optimal stimuli determined by mixed-integer optimal control.

  • Corresponding differential states.


Source Code

C

The differential equations in C code: 

double myu = p[17] * (1.0 + u[0]* ( p[19] - 1.0) ) ;
 
rhs[0] = p[0]
         + p[1]*xd[0]
         - p[2]*xd[0]*xd[1]/(xd[0]+p[3])
         - p[4]*xd[0]*xd[2]/(xd[0]+p[5]);
 
rhs[1] = p[6]*xd[0]
         - p[7]*xd[1]/(xd[1]+p[8]);
 
rhs[2] = p[9]*xd[1]*xd[2]*xd[3]/(xd[3]+p[10])
         + p[18]*p[11]*xd[1]
         + p[12]*xd[0]
         - p[13]*xd[2]/(myu*xd[2]+p[14])
         - p[15]*xd[2]/(xd[2]+p[16])
         + 0.1*xd[3];
 
rhs[3] = -p[9]*xd[1]*xd[2]*xd[3]/(xd[3]+p[10])
         + p[15]*xd[2]/(xd[2]+p[16])
         - 0.1*xd[3];

Variants

Use of two control functions.

References

<bibreferences/>

Retrieved from "https://mintoc.de/index.php?title=Annihilation_of_calcium_oscillations&oldid=239"