Difference between revisions of "Urethane"

From mintOC
Jump to: navigation, search
(→‎Mathematical formulation)
(→‎References)
Line 219: Line 219:
  
 
== References ==
 
== References ==
−
To be added.
+
 
−
<!--
+
<span id="KoerkelDiss">[1]</span> "Numerische Methoden für Optimale Versuchsplanungsprobleme bei nichtlinearen DAE-Modellen " by S. Körkel <br>
−
<biblist />
+
<span id="Koerkel2000">[2]</span> "Numerical methods for optimum experimental design in DAE systems" by I. Bauer, H.G. Bock, S. Körkel and J.P. Schlöder <br>
−
-->
+
<span id="OEDUDE">[3]</span> "Optimal Experimental Design for Universal Differential Equations" by C. Plate, C.J. Martensen and S. Sager
  
 
<!--List of all categories this page is part of. List characterization of solution behavior, model properties, ore presence of implementation details (e.g., AMPL for AMPL model) here -->
 
<!--List of all categories this page is part of. List characterization of solution behavior, model properties, ore presence of implementation details (e.g., AMPL for AMPL model) here -->

Revision as of 13:30, 12 November 2024

Urethane
State dimension: 1
Differential states: 11
Discrete control functions: 2
Path constraints: 4
Interior point equalities: 11


This page describes the Optimal Experimental Design Problem for the Urethane Reaction. The following formulation is taken from the PhD thesis "Numerische Methoden für Optimale Versuchsplanungsprobleme bei nichtlinearen DAE-Modellen" by Stefan Körkel.

Chemical background

The reaction scheme of the urethane reaction is as follows:

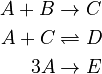
\begin{align} A + B &\rightarrow C \\ A + C &\rightleftharpoons D \\ 3A &\rightarrow E \end{align}

For ease of notation the chemical substances use the abbreviations

Letter Substance
A Phenyl Isocyanate
B Butanol
C Urethane (Main Product)
D Allophanate (Secondary Product)
E Isocyanurate (Byproduct)
L Dimethyl Sulfoxide

The reactor for the urethane reaction is a stirred tank and can be operated as a batch or semi-batch process with up to two feeds. In the reactor, phenyl isocyanate and butanol can be initially charged in the solvent dimethyl sulfoxide. In feed 1, phenyl isocyanate in dimethyl sulfoxide can be added, and in feed 2, butanol in dimethyl sulfoxide can be added. The internal temperature of the reactor is controllable.

Mathematical formulation

We can model this process using a nonlinear DAE model

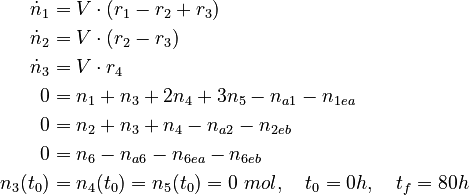
\begin{align} \dot{n}_1 &= V \cdot (r_1 - r_2 + r_3) \\ \dot{n}_2 &= V \cdot (r_2 - r_3) \\ \dot{n}_3 &= V \cdot r_4 \\ 0 &= n_1 + n_3 + 2n_4 + 3n_5 - n_{a1} - n_{1ea} \\ 0 &= n_2 + n_3 + n_4 - n_{a2} - n_{2eb} \\ 0 &= n_6 - n_{a6} - n_{6ea} - n_{6eb} \\ n_3(t_0) &= n_4(t_0) = n_5(t_0) = 0 \ mol, \quad t_0 = 0h, \quad t_f = 80h \end{align}

with

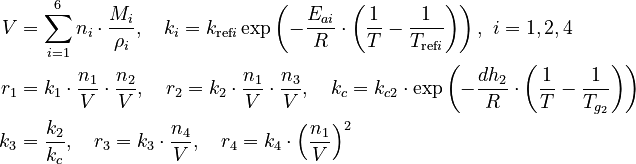
\begin{align} V &= \sum_{i=1}^6 n_i \cdot \frac{M_i}{\rho_i}, \quad k_i = k_{\text{ref}i} \exp \left( -\frac{E_{ai}}{R} \cdot \left( \frac{1}{T} - \frac{1}{T_{\text{ref}i}} \right) \right), \ i=1,2,4 \\ r_1 &= k_1 \cdot \frac{n_1}{V} \cdot \frac{n_2}{V}, \quad r_2 = k_2 \cdot \frac{n_1}{V} \cdot \frac{n_3}{V}, \quad k_c = k_{c2} \cdot \exp \left( - \frac{dh_2}{R} \cdot \left( \frac{1}{T} - \frac{1}{T_{g_2}} \right) \right) \\ k_3 &= \frac{k_2}{k_c}, \quad r_3 = k_3 \cdot \frac{n_4}{V}, \quad r_4 = k_4 \cdot \left( \frac{n_1}{V} \right)^2 \end{align}

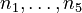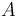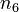The molar numbers n_1,\ldots,n_5 of the species A to E and n_6 of the solvent 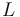L are the state variables of the DAE system. There are eight unknown parameters in this model:

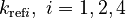
  • the steric factors k_{\text{ref}i}, \ i=1,2,4
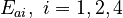
  • the activation energies E_{ai}, \ i=1,2,4
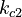  • the equilibrium constant k_{c2} (for the reference temperature T_{g2})
  • the reaction enthalpy dh_2 of the reversible reaction

    • The two feeds are modelled by two monotonously increasing control functions

    \text{feed}_a,\text{feed}_b: \ [t_0,t_f] \rightarrow [0,1]

    describing the profiles of the accumulated feeds. Multiplied with the initial molar numbers within the feed vessels, we get the feed molar numbers:

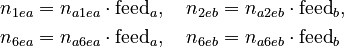
    \begin{align} n_{1ea} &= n_{a1ea} \cdot \text{feed}_a, \quad n_{2eb} = n_{a2eb} \cdot \text{feed}_b, \\ n_{6ea} &= n_{a6ea} \cdot \text{feed}_a, \quad n_{6eb} = n_{a6eb} \cdot \text{feed}_b \end{align}

    The third control function is the temperature profile

    T: [t_0,t_f] \rightarrow [293.16 \ K, \ 473.16 \ K]

    Each experiment lasts 80 h. The beginning is Monday, 8 pm, the end Thursday, 4 pm. During the nights, the feed rates and the heating=cooling rate have to be zero due to safety rules. Further control variables for experimental design are

  • the mole ratios MV_1 \in [0.1, 10], \ MV_2 \in [0, 1000], and MV_3 \in [0, 10]
  • the parts of active ingredients g_a \in [0, 0.8], \ g_{aea} \in [0, 0.9], and g_{aeb} \in [0, 1]
  • the initial volume V_a \in [0 m^3 , 0.00075 m^3 ] of the species in the reactor.

    • These quantities are connected to the initial molar numbers as follows

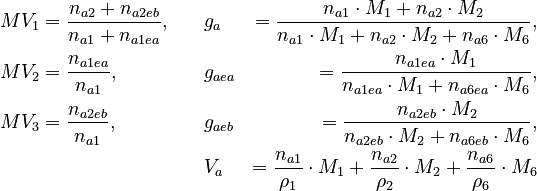
    \begin{align} MV_1 &= \frac{n_{a2}+n_{a2eb}}{n_{a1} + n_{a1ea}}, \quad && g_a &= \frac{n_{a1} \cdot M_1 + n_{a2} \cdot M_2}{n_{a1} \cdot M_1 + n_{a2} \cdot M_2 + n_{a6} \cdot M_6}, \\ MV_2 &= \frac{n_{a1ea}}{n_{a1}}, && g_{aea} &= \frac{n_{a1ea} \cdot M_1}{n_{a1ea} \cdot M_1 + n_{a6ea} \cdot M_6}, \\ MV_3 &= \frac{n_{a2eb}}{n_{a1}}, \quad && g_{aeb} &= \frac{n_{a2eb} \cdot M_2}{n_{a2eb} \cdot M_2 + n_{a6eb} \cdot M_6}, \\ & && V_a &= \frac{n_{a1}}{\rho_1} \cdot M_1 + \frac{n_{a2}}{\rho_2} \cdot M_2 + \frac{n_{a6}}{\rho_6} \cdot M_6 \end{align}

    The remaining quantities are constants and shown in the parameter section. Three measurement methods are available:

  • titration, measuring mass percent of phenylisocyanate with a standard deviation of the measurement error of 0.5,
  • HPLC1, giving mass percent of urethane and allophanate with standard deviations 0.5 resp. 0.005,
  • HPLC2, for mass percent of isocyanurate with standard deviation 0.0005

    • In each experiment, 16 measurements can be selected out of 30 possible ones. We parametrize the time depending control functions using piecewise linear and continuous polynomials. Altogether we have 90 experimental design variables for each experiment: 7 control variables, 7 initial molar numbers, 30 weights on the measurements, and 46 variables due to the parametrization of the control functions.

    Parameters

    Intial Values
    MV_1 1.0
    MV_2 0.3
    MV_3 0.3
    g_a 0.75
    g_{aea} 0.5
    g_{aeb} 0.4
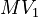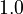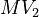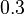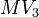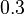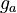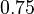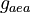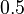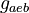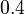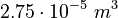    V_a 2.75\cdot 10^{-5} \ m^3


    Constants
    Molar Mass Density Reference Temperature
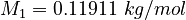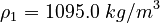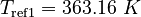    \quad M_1 = 0.11911 \ kg/mol \quad \rho_1 = 1095.0 \ kg/m^3 T_{\text{ref}1} = 363.16 \ K
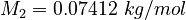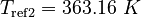    M_2 = 0.07412 \ kg/mol \rho_2 = 809.0 \ kg/m^3 T_{\text{ref}2} = 363.16 \ K
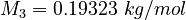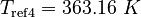    M_3 = 0.19323 \ kg/mol \rho_3 = 1415.0 \ kg/m^3 T_{\text{ref}4} = 363.16 \ K
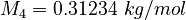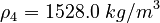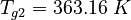    M_4 = 0.31234 \ kg/mol \rho_4 = 1528.0 \ kg/m^3 T_{g2} = 363.16 \ K
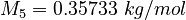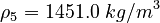    M_5 = 0.35733 \ kg/mol \rho_5 = 1451.0 \ kg/m^3 molar gas constant
    R = 8.314 \ J/(K\cdot mol)
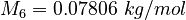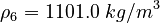    M_6 = 0.07806 \ kg/mol \rho_6 = 1101.0 \ kg/m^3

    Optimal Experimental Design Problem

    To be specified.


    Miscellaneous and Further Reading

    To be specified.

    References

    [1] "Numerische Methoden für Optimale Versuchsplanungsprobleme bei nichtlinearen DAE-Modellen " by S. Körkel
    [2] "Numerical methods for optimum experimental design in DAE systems" by I. Bauer, H.G. Bock, S. Körkel and J.P. Schlöder
    [3] "Optimal Experimental Design for Universal Differential Equations" by C. Plate, C.J. Martensen and S. Sager

    Retrieved from "https://mintoc.de/index.php?title=Urethane&oldid=2419"