Difference between revisions of "Bang-bang approximation of a traveling wave"

From mintOC
Jump to: navigation, search
(Added reference solution)
m (Added reference)
Line 1: Line 1:
−
The following problem is an academic example of a PDE constrained optimal control problem with integer control constraints.
+
The following problem is an academic example of a PDE constrained optimal control problem with integer control constraints
−
<!-- and was introduced in <bibref>Hante2009</bibref>. -->
+
and was introduced in <bibref>Hante2009</bibref>.  
  
 
The control task consists of choosing the boundary value of a transport equation from the extremal values of a traveling  
 
The control task consists of choosing the boundary value of a transport equation from the extremal values of a traveling  

Revision as of 13:29, 16 August 2010

The following problem is an academic example of a PDE constrained optimal control problem with integer control constraints and was introduced in <bibref>Hante2009</bibref>.

The control task consists of choosing the boundary value of a transport equation from the extremal values of a traveling wave such that the 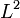L^2-distance between the traveling wave and the resulting flow is minimized.


Mathematical formulation

\begin{array}{ll} \displaystyle \min_{x, q} & \displaystyle \int_0^1\int_0^1 |x(t,s)-x_d(t,s)|^2\,ds\,dt + c \bigvee_0^1 q(t)\,dt \\[1.5ex] \mbox{s.t.} & \displaystyle \frac{\partial}{\partial t}x(t,s)+\frac{\partial}{\partial s}x(t,s) = 0,\quad 0<s<1,~0<t<1\\[1.5ex] & \displaystyle x(t,0) = q(t),\quad 0<t<1 \\ & \displaystyle x(0,s) = x_d(0,s),\quad 0<s<1 \\ & \displaystyle q(t) \in \{0,1\},\quad 0<t<1 \\ \end{array}

where

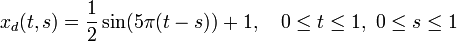
x_d(t,s)=\frac12\sin(5\pi(t-s))+1,\quad 0\leq t \leq 1,~0\leq s\leq 1

is the traveling wave (oscillating between 0 and 1), 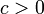c>0 is a (small) regularization parameter and 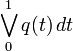\bigvee_0^1 q(t)\,dt denotes the variation of q(\cdot) over the interval [0,1]. Thereby, the solution of the transport equation has to be understood in the usual weak sense defined by the characteristic equations.


Reference Solution

For 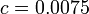c=0.0075 the best known solution is given by

q^*(t)=\chi_{[0,0.2]}(t)+\chi_{[0.4,0.6]}(t)+\chi_{[0.8,1]}(t),\quad 0\leq t\leq 1

where \chi_{[a,b]}(t) denotes the indicator function of the interval [a,b].


References

<bibreferences/>

Retrieved from "https://mintoc.de/index.php?title=Bang-bang_approximation_of_a_traveling_wave&oldid=567"