Difference between revisions of "Lotka Volterra fishing problem"

From mintOC
Jump to: navigation, search
(Table ausprobiert)
Line 2: Line 2:
 
|nd        = 1
 
|nd        = 1
 
|nx        = 3
 
|nx        = 3
−
|nz        = 0
 
−
|nu        = 0
 
 
|nw        = 1
 
|nw        = 1
−
|np        = 0
 
−
|nrho      = 0
 
−
|nc        = 0
 
−
|nri      = 0
 
 
|nre      = 3
 
|nre      = 3
 
}}
 
}}
 +
 +
<table width="100%" cellspacing="10px">
 +
<tr valign="top">
 +
<td width="80%" >
  
 
The '''Lotka Volterra fishing problem''' looks for an optimal fishing strategy to be performed on a fixed time horizon to bring the biomasses of both predator as prey fish to a prescribed steady state. The problem was set up as a small-scale benchmark problem.  
 
The '''Lotka Volterra fishing problem''' looks for an optimal fishing strategy to be performed on a fixed time horizon to bring the biomasses of both predator as prey fish to a prescribed steady state. The problem was set up as a small-scale benchmark problem.  
Line 18: Line 16:
  
 
The optimal solution contains a singular arc, making the Lotka Volterra fishing problem an ideal candidate for benchmarking of algorithms.
 
The optimal solution contains a singular arc, making the Lotka Volterra fishing problem an ideal candidate for benchmarking of algorithms.
 +
 +
<!-- Do not edit between this comment and the next '<td>' tag! -->
 +
</td>
 +
<td width="20%">
 +
</td>
 +
</tr>
 +
</table>
 +
  
 
== Mathematical formulation ==
 
== Mathematical formulation ==

Revision as of 12:00, 11 July 2008

Lotka Volterra fishing problem
State dimension: 1
Differential states: 3
Discrete control functions: 1
Interior point equalities: 3


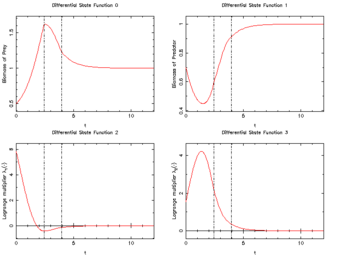
The Lotka Volterra fishing problem looks for an optimal fishing strategy to be performed on a fixed time horizon to bring the biomasses of both predator as prey fish to a prescribed steady state. The problem was set up as a small-scale benchmark problem. The well known Lotka Volterra equations for a predator-prey system have been augmented by an additional linear term, relating to fishing by man. The control can be regarded both in a relaxed, as in a discrete manner, corresponding to a part of the fleet, or the full fishing fleet.

It is thus an ODE model with a single integer control function. The interior point equality conditions fix the initial values of the differential states.

The optimal solution contains a singular arc, making the Lotka Volterra fishing problem an ideal candidate for benchmarking of algorithms.


Mathematical formulation

For t \in [t_0, t_f] almost everywhere the mixed-integer optimal control problem is given by

\begin{array}{llcl} \displaystyle \min_{x, w} & x_2(t_f) \\[1.5ex] \mbox{s.t.} & \dot{x}_0(t) & = & x_0(t) - x_0(t) x_1(t) - \; c_0 x_0(t) \; w(t), \\ & \dot{x}_1(t) & = & - x_1(t) + x_0(t) x_1(t) - \; c_1 x_1(t) \; w(t), \\ & \dot{x}_2(t) & = & (x_0(t) - 1)^2 + (x_1(t) - 1)^2, \\[1.5ex] & x(0) &=& x_0, \\ & w(t) &\in& \{0, 1\}. \end{array}

Initial values and parameters

These fixed values are used within the model.

\begin{array}{rcl} [t_0, t_f] &=& [0, 12],\\ (c_0, c_1) &=& (0.4, 0.2),\\ x_0 &=& (0.5, 0.7, 0)^T. \end{array}

Reference Solutions

States


The two differential states and corresponding adjoint variables in the indirect approach

Source Code

C

The differential equations in C code: 

/* steady state with u == 0 */
double ref0 = 1, ref1 = 1;
 
/* Biomass of prey */
rhs[0] =   xd[0] - xd[0]*xd[1] - p[0]*u[0]*xd[0];
/* Biomass of predator */
rhs[1] = - xd[1] + xd[0]*xd[1] - p[1]*u[0]*xd[1];
/* Deviation from reference trajectory */
rhs[2] = (xd[0]-ref0)*(xd[0]-ref0) + (xd[1]-ref1)*(xd[1]-ref1);

AMPL

The model in AMPL code with a collocation method. We need a model file lotka_ampl.mod, 

# ----------------------------------------------------
# Solve Lotka Volterra fishing problem via collocation
# ----------------------------------------------------
 
param T    > 0;
param nt   > 0;
param c1   > 0;
param c2   > 0;
param ref1 > 0;
param ref2 > 0;
param dt := T / nt;
set I:= 0..nt-1;
 
var x {I, 1..2} >= 0;
var w {I} binary;
 
minimize Deviation:
   dt * sum {i in I} ( (x[i,1] - ref1)*(x[i,1] - ref1) 
	                   + (x[i,2] - ref2)*(x[i,2] - ref2) ) ;
 
subj to ODE_DISC_1 {i in I diff {0}}:
   x[i,1] = x[i-1,1] + dt * ( x[i-1,1] - x[i-1,1]*x[i-1,2] - x[i-1,1]*c1*w[i-1] );
 
subj to ODE_DISC_2 {i in I diff {0}}:
   x[i,2] = x[i-1,2] + dt * ( - x[i-1,2] + x[i-1,1]*x[i-1,2] - x[i-1,2]*c2*w[i-1] );

a data file lotka_ampl.dat, 

# ------------------------------------
# Data: Lotka Volterra fishing problem
# ------------------------------------
 
# Problem parameters
param T := 12.0;
param nt := 101;
param c1 := 0.4;
param c2 := 0.2;
param ref1 := 1.0;
param ref2 := 1.0;
 
# Initial values differential states
let x[0,1] := 0.5;
let x[0,2] := 0.7;
fix x[0,1];
fix x[0,2];
 
# Initial values control
let {i in I} w[i] := 0.0;
 
param mysum;

and a running script lotka_ampl.run, 

# ----------------------------------------------------
# Solve Lotka Volterra fishing problem via collocation
# ----------------------------------------------------
 
model ampl_lotka.mod;
data ampl_lotka.dat;
 
option solver bonmin;
 
solve;

Miscellaneous

The Lotka Volterra fishing problem was introduced by Sebastian Sager in a proceedings paper <bibref>Sager2006</bibref> and revisited in his PhD thesis <bibref>Sager2005</bibref>. These are also the references to look for more details.

References

<bibreferences/>

Retrieved from "https://mintoc.de/index.php?title=Lotka_Volterra_fishing_problem&oldid=66"