Difference between revisions of "Bioreactor"

From mintOC
Jump to: navigation, search
Line 28: Line 28:
 
<math>\mu = \mu_{m}*(1-P/P_{m})*S/(K_m+S+S^2/K_i)</math>
 
<math>\mu = \mu_{m}*(1-P/P_{m})*S/(K_m+S+S^2/K_i)</math>
  
−
In this section the dynamic model, that describes the physical or technical process of interest, should be described. First the differential equation should be written down. Then the states, inputs, and parameters should be declared (Dimension, Type (integer, real, binary, ...)). Finally the parameters that are not free in the optimization and the coefficients should be stated in an extra table or list. All equations and functions are defined over an interval <math>I \subset \R</math>. Initial values and free parameters are taken into account later in the Optimal Control Problem.
+
The fixed parameters (constants) of the model are:
−
 
+
−
 
+
−
The parameter (coefficient) <math> p </math> could be stated in a table, if it is fixed.
+
  
 
{| class="wikitable"
 
{| class="wikitable"
−
|+Parameter(s)
+
|+Parameters
 
|-
 
|-
 
|Name
 
|Name
Line 41: Line 38:
 
|Unit
 
|Unit
 
|-
 
|-
−
|Parameter
+
|Dilution
−
|<math>p</math>
+
|<math>D</math>
−
|23
+
|0.15
 
|[-]
 
|[-]
 +
|-
 +
|Dilution
 +
|<math>D</math>
 +
|0.15
 +
|[-]
 +
|-
 +
|Dilution
 +
|<math>D</math>
 +
|0.15
 +
|[-]
 +
|-
 
|}
 
|}
 +
 +
const double Ki      = 22.0;
 +
    const double Km      = 1.2 ;
 +
    const double Pm      = 50.0;
 +
    const double Yxs    = 0.4 ;
 +
    const double alpha  = 2.2 ;
 +
    const double beta    = 0.2 ;
 +
    const double mum    = 0.48;
  
 
This would result in an right hand side function <math>f(x,u)</math> in this case, because there are no free parameters. Of course one could also specify an implicit DAE system (<math>F(\dot{x},x,u,p,t)=0</math>), where it just hast to be said which states are differential and which are algebraic.
 
This would result in an right hand side function <math>f(x,u)</math> in this case, because there are no free parameters. Of course one could also specify an implicit DAE system (<math>F(\dot{x},x,u,p,t)=0</math>), where it just hast to be said which states are differential and which are algebraic.

Revision as of 16:42, 8 December 2015

The bioreactor example is an easy bioreactor with an substrate that is converted to a product by the biomass in the reactor. It has three states and a control that is describing the feed concentration of substrate. It is taken from the examples folder of the ACADO toolkit described in: 

Houska, Boris, Hans Joachim Ferreau, and Moritz Diehl. "ACADO toolkit—An open‐source framework for automatic control and dynamic optimization."
Optimal Control Applications and Methods 32.3 (2011): 298-312.

Originally the problem seems to be motivated by: 

VERSYCK, KARINA J., and JAN F. VAN IMPE. "Feed rate optimization for fed-batch bioreactors: From optimal process performance to optimal parameter estimation."
Chemical Engineering Communications 172.1 (1999): 107-124.

Model Formulation

The dynamic model is an ODE model:

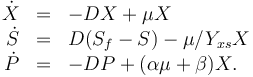
\begin{array}{rcl} \dot{X}&=&-DX+\mu X \\ \dot{S}&=& D(S_{f}-S)-\mu /Y_{xs} X \\ \dot{P}&=&-DP+ (\alpha \mu +\beta) X. \end{array}

The three states describe the concentration of the biomass (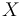X), the substrate (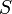S), and the product (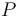P) in the reactor. In steady state the feed and outlet are equal and dilute all three concentrations with a ratio 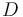D. The biomass grows with a rate 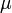\mu, while it eats up the substrate with the rate 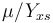\mu/Y_{xs} and produces product at a rate 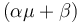(\alpha \mu +\beta). The rate 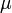\mu is given by:

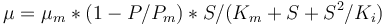
\mu = \mu_{m}*(1-P/P_{m})*S/(K_m+S+S^2/K_i)

The fixed parameters (constants) of the model are:

Parameters
Name Symbol Value Unit
Dilution 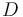D 0.15 [-]
Dilution D 0.15 [-]
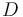
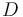
Dilution D 0.15 [-]

const double Ki = 22.0; 

   const double Km      = 1.2 ; 
   const double Pm      = 50.0;
   const double Yxs     = 0.4 ;
   const double alpha   = 2.2 ;
   const double beta    = 0.2 ;
   const double mum     = 0.48;

This would result in an right hand side function 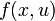f(x,u) in this case, because there are no free parameters. Of course one could also specify an implicit DAE system (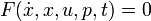F(\dot{x},x,u,p,t)=0), where it just hast to be said which states are differential and which are algebraic.

Retrieved from "https://mintoc.de/index.php?title=Bioreactor&oldid=873"