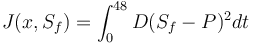Difference between revisions of "Bioreactor"

From mintOC
Jump to: navigation, search
Line 89: Line 89:
 
  \displaystyle \min_{x,S_f} & J(x,S_f)\\[1.5ex]
 
  \displaystyle \min_{x,S_f} & J(x,S_f)\\[1.5ex]
 
  \mbox{s.t.} & \dot{x}  =  f(x,S_f), \forall \, t \in [0,48]\\
 
  \mbox{s.t.} & \dot{x}  =  f(x,S_f), \forall \, t \in [0,48]\\
−
  & x(0) = [6.5,12,22]^T \\
+
  & x(0) = (6.5,12,22)^T \\
 
  & x \in \R^3,\,S_f \in [28.7,40].
 
  & x \in \R^3,\,S_f \in [28.7,40].
 
\end{array}  
 
\end{array}  
Line 95: Line 95:
 
</p>
 
</p>
  
−
This is the most general formulation, where the initial value, parameters, and inputs are free. The states and inputs are vectors (or matrices) of functions while the parameters are just a vector of variables. If the initial (or final) state is fixed, one just adds a constraint <math>x(t_0)=x_0</math> and specifies the value(s) of <math>x_0</math> in a list or table.
+
=== Objective ===
−
If the parameters are fixed, then one just removes them from the list of optimization variables and states their values in a list (same for point conditions inside of the interval <math>I</math>). If the OCP is a parameter estimation problem without inputs,
+
<p>
−
the inputs just dont appear in the problem above at all, neither as optimization variable nor as part of the constraints. In contrast if they are just fixed this is done by the equality constraints. In this setup the above problem is very general and by
+
<math>
−
stating the different objective functions and constraint functions one can cover a wide range of OCPs.
+
J(x,S_f)=\int_0^{48}D(S_f-P)^2dt
 +
</math>
 +
</p>

Revision as of 17:06, 8 December 2015

The bioreactor example is an easy bioreactor with an substrate that is converted to a product by the biomass in the reactor. It has three states and a control that is describing the feed concentration of substrate. It is taken from the examples folder of the ACADO toolkit described in: 

Houska, Boris, Hans Joachim Ferreau, and Moritz Diehl. "ACADO toolkit—An open‐source framework for automatic control and dynamic optimization."
Optimal Control Applications and Methods 32.3 (2011): 298-312.

Originally the problem seems to be motivated by: 

VERSYCK, KARINA J., and JAN F. VAN IMPE. "Feed rate optimization for fed-batch bioreactors: From optimal process performance to optimal parameter estimation."
Chemical Engineering Communications 172.1 (1999): 107-124.

Model Formulation

The dynamic model is an ODE model:

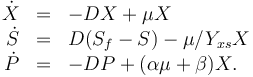
\begin{array}{rcl} \dot{X}&=&-DX+\mu X \\ \dot{S}&=& D(S_{f}-S)-\mu /Y_{xs} X \\ \dot{P}&=&-DP+ (\alpha \mu +\beta) X. \end{array}

The three states describe the concentration of the biomass (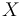X), the substrate (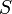S), and the product (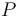P) in the reactor. In steady state the feed and outlet are equal and dilute all three concentrations with a ratio 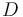D. The biomass grows with a rate 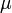\mu, while it eats up the substrate with the rate 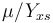\mu/Y_{xs} and produces product at a rate 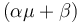(\alpha \mu +\beta). The rate 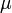\mu is given by:

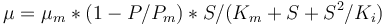
\mu = \mu_{m}*(1-P/P_{m})*S/(K_m+S+S^2/K_i)

The fixed parameters (constants) of the model are as follows.

Parameters
Name Symbol Value Unit
Dilution 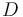D 0.15 [-]
Rate coefficient 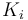K_i 22 [-]
Rate coefficient 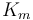K_m 1.2 [-]
Rate coefficient 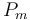P_m 50 [-]
Substrate to Biomass rate 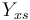Y_{xs} 0.4 [-]
Linear slope 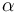\alpha 2.2 [-]
Linear intercept 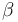\beta 0.2 [-]
Maximal growth rate 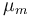\mu_m 0.48 [-]

Optimal Control Problem

Writing shortly for the states in vector notation 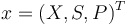x=(X,S,P)^T the OCP reads:

\begin{array}{cl} \displaystyle \min_{x,S_f} & J(x,S_f)\\[1.5ex] \mbox{s.t.} & \dot{x} = f(x,S_f), \forall \, t \in [0,48]\\ & x(0) = (6.5,12,22)^T \\ & x \in \R^3,\,S_f \in [28.7,40]. \end{array}

Objective

J(x,S_f)=\int_0^{48}D(S_f-P)^2dt

Retrieved from "https://mintoc.de/index.php?title=Bioreactor&oldid=893"