Difference between revisions of "Bioreactor"

From mintOC
Jump to: navigation, search
Line 101: Line 101:
 
</math>
 
</math>
 
</p>
 
</p>
 +
 +
== Reference Solution ==
 +
 +
Here we first give the reference solution according to the ACADO example. In the next section the C++ source code for this solution is given.
 +
 +
<gallery caption="Reference solution plots" widths="271px" heights="379px" perrow="2">
 +
| Optimal solution for the ACADO example.
 +
</gallery>
 +
 +
== Source Code ==
 +
 +
In this section one can provide the source code of the implementation, that solved the problem and produced the reference solution. This should be done by providing source files.

Revision as of 15:24, 9 December 2015

The bioreactor example is an easy bioreactor with an substrate that is converted to a product by the biomass in the reactor. It has three states and a control that is describing the feed concentration of substrate. It is taken from the examples folder of the ACADO toolkit described in: 

Houska, Boris, Hans Joachim Ferreau, and Moritz Diehl. "ACADO toolkit—An open‐source framework for automatic control and dynamic optimization."
Optimal Control Applications and Methods 32.3 (2011): 298-312.

Originally the problem seems to be motivated by: 

VERSYCK, KARINA J., and JAN F. VAN IMPE. "Feed rate optimization for fed-batch bioreactors: From optimal process performance to optimal parameter estimation."
Chemical Engineering Communications 172.1 (1999): 107-124.

Model Formulation

The dynamic model is an ODE model:

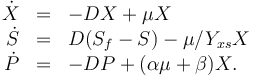
\begin{array}{rcl} \dot{X}&=&-DX+\mu X \\ \dot{S}&=& D(S_{f}-S)-\mu /Y_{xs} X \\ \dot{P}&=&-DP+ (\alpha \mu +\beta) X. \end{array}

The three states describe the concentration of the biomass (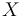X), the substrate (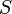S), and the product (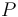P) in the reactor. In steady state the feed and outlet are equal and dilute all three concentrations with a ratio 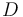D. The biomass grows with a rate 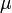\mu, while it eats up the substrate with the rate 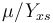\mu/Y_{xs} and produces product at a rate 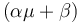(\alpha \mu +\beta). The rate 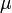\mu is given by:

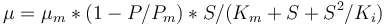
\mu = \mu_{m}*(1-P/P_{m})*S/(K_m+S+S^2/K_i)

The fixed parameters (constants) of the model are as follows.

Parameters
Name Symbol Value Unit
Dilution 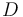D 0.15 [-]
Rate coefficient 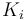K_i 22 [-]
Rate coefficient 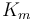K_m 1.2 [-]
Rate coefficient 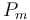P_m 50 [-]
Substrate to Biomass rate 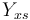Y_{xs} 0.4 [-]
Linear slope 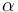\alpha 2.2 [-]
Linear intercept 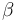\beta 0.2 [-]
Maximal growth rate 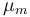\mu_m 0.48 [-]

Optimal Control Problem

Writing shortly for the states in vector notation 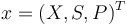x=(X,S,P)^T the OCP reads:

\begin{array}{cl} \displaystyle \min_{x,S_f} & J(x,S_f)\\[1.5ex] \mbox{s.t.} & \dot{x} = f(x,S_f), \forall \, t \in [0,48]\\ & x(0) = (6.5,12,22)^T \\ & x \in \R^3,\,S_f \in [28.7,40]. \end{array}

Objective

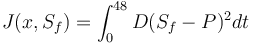
J(x,S_f)=\int_0^{48}D(S_f-P)^2dt

Reference Solution

Here we first give the reference solution according to the ACADO example. In the next section the C++ source code for this solution is given.

  • Reference solution plots

Source Code

In this section one can provide the source code of the implementation, that solved the problem and produced the reference solution. This should be done by providing source files.

Retrieved from "https://mintoc.de/index.php?title=Bioreactor&oldid=977"