Category:Complementarity constraints

From mintOC
Revision as of 11:11, 23 January 2016 by JonasSchulze (Talk | contribs) (Text replacement - "<bibreferences/>" to "<biblist />")

(diff) ← Older revision | Latest revision (diff) | Newer revision → (diff)
Jump to: navigation, search

This category contains optimization problems with complementarity constraints (MPCCs), for generic variables / functions 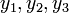y_1, y_2, y_3 in the form of

\begin{array}{llcl} \displaystyle \min_{y_1, y_2, y_3} & & & \Phi(y_1, y_2, y_3) \\[1.5ex] \mbox{s.t.} & 0 & = & F ( y_1, y_2, y_3), \\ & 0 & \le & C ( y_1, y_2, y_3), \\ & 0 & \le & y_1 \perp y_2 \ge 0, \end{array}

The complementarity operator 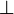\perp implies the disjunctive behavior

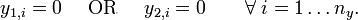
y_{1,i} = 0 \quad{\mbox{ OR } }\quad y_{2,i} = 0 \quad \quad \forall \; i = 1 \dots n_y.

MPCCs may arise from a reformulation of a bilevel optimization problem by writing the optimality conditions of the inner problem as variational constraints of the outer optimization problem, or from a special treatment of state-dependent switches, [Baumrucker2009]Author: B.T. Baumrucker; L.T. Biegler
Journal: Journal of Process Control
Note: Special Section on Hybrid Systems: Modeling, Simulation and Optimization
Number: 8
Pages: 1248--1256
Title: MPEC strategies for optimization of a class of hybrid dynamic systems
Volume: 19
Year: 2009
Link to Google Scholar. Note that all MPCCs can be reformulated as MPECs.


References

[Baumrucker2009]B.T. Baumrucker; L.T. Biegler (2009): MPEC strategies for optimization of a class of hybrid dynamic systems. Journal of Process Control, 19, 1248--1256Link to Google Scholar

This category currently contains no pages or media.

Retrieved from "https://mintoc.de/index.php?title=Category:Complementarity_constraints&oldid=1385"