Lotka Volterra fishing problem

Lotka Volterra fishing problem
State dimension:	1
Differential states:	3
Discrete control functions:	1
Interior point equalities:	3

The Lotka Volterra fishing problem looks for an optimal fishing strategy to be performed on a fixed time horizon to bring the biomasses of both predator as prey fish to a prescribed steady state. The problem was set up as a small-scale benchmark problem. The well known Lotka Volterra equations for a predator-prey system have been augmented by an additional linear term, relating to fishing by man. The control can be regarded both in a relaxed, as in a discrete manner, corresponding to a part of the fleet, or the full fishing fleet.

It is thus an ODE model with a single integer control function. The interior point equality conditions fix the initial values of the differential states.

The optimal solution contains a singular arc, making the Lotka Volterra fishing problem an ideal candidate for benchmarking of algorithms.

Mathematical formulation

For $t \in [t_0, t_f]$ almost everywhere the mixed-integer optimal control problem is given by

$\begin{array}{llcl} \displaystyle \min_{x, w} & x_2(t_f) \\[1.5ex] \mbox{s.t.} & \dot{x}_0(t) & = & x_0(t) - x_0(t) x_1(t) - \; c_0 x_0(t) \; w(t), \\ & \dot{x}_1(t) & = & - x_1(t) + x_0(t) x_1(t) - \; c_1 x_1(t) \; w(t), \\ & \dot{x}_2(t) & = & (x_0(t) - 1)^2 + (x_1(t) - 1)^2, \\[1.5ex] & x(0) &=& x_0, \\ & w(t) &\in& \{0, 1\}. \end{array}$

Initial values and parameters

These fixed values are used within the model.

$\begin{array}{rcl} [t_0, t_f] &=& [0, 12],\\ (c_0, c_1) &=& (0.4, 0.2),\\ x_0 &=& (0.5, 0.7, 0)^T. \end{array}$

Reference Solutions

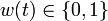If the problem is relaxed, i.e., we demand $w(t) \in [0, 1]$ instead of $w(t) \in \{0,1\}$, the optimal solution can be determined by means of Pontryagins maximum principle. The optimal solution contains a singular arc, as can be seen in the plot of the optimal control. The two differential states and corresponding adjoint variables in the indirect approach are also displayed. A different approach to solving the relaxed problem is by using a direct method such as collocation or Bock's direct multiple shooting method. Optimal solutions for different control discretizations are also plotted in the leftmost figure.

The optimal objective value of this relaxed problem is 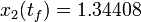$x_2(t_f) = 1.34408$. As follows from MIOC theory<bibref>Sager2008</bibref> this is the best lower bound on the optimal value of the original problem with the integer restriction on the control function. In other words, this objective value can be approximated arbitrarily close, if the control only switches often enough between 0 and 1. As no optimal solution exists, two suboptimal ones are shown, one with only two switches and an objective function value of 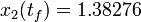$x_2(t_f) = 1.38276$, and one with 56 switches and $x_2(t_f) = 1.34416$.

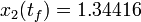• Reference solution plots
• 

  Optimal relaxed control determined by an indirect approach and by a direct approach on different control discretization grids.

• 

  Differential states and corresponding adjoint variables in the indirect approach.

• 

  Control and differential states with only two switches.

• 

  Control and differential states with 56 switches.

Source Code

C

The differential equations in C code:

/* steady state with u == 0 */
double ref0 = 1, ref1 = 1;
 
/* Biomass of prey */
rhs[0] =   xd[0] - xd[0]*xd[1] - p[0]*u[0]*xd[0];
/* Biomass of predator */
rhs[1] = - xd[1] + xd[0]*xd[1] - p[1]*u[0]*xd[1];
/* Deviation from reference trajectory */
rhs[2] = (xd[0]-ref0)*(xd[0]-ref0) + (xd[1]-ref1)*(xd[1]-ref1);

AMPL

The model in AMPL code for a fixed control discretization grid with a collocation method. We need a model file lotka_ampl.mod,

# ----------------------------------------------------------------
# Lotka Volterra fishing problem with collocation (explicit Euler)
# (c) Sebastian Sager
# ----------------------------------------------------------------
 
param T    > 0;
param nt   > 0;
param c1   > 0;
param c2   > 0;
param ref1 > 0;
param ref2 > 0;
param dt := T / (nt-1);
set I:= 0..nt;
 
var x {I, 1..2} >= 0;
var w {I} >= 0, <= 1 binary;
 
minimize Deviation:
	  0.5 * dt * ( (x[0,1] - ref1)*(x[0,1] - ref1) + (x[0,2] - ref2)*(x[0,2] - ref2) )
	+ 0.5 * dt * ( (x[nt,1] - ref1)*(x[nt,1] - ref1) + (x[nt,2] - ref2)*(x[nt,2] - ref2) )
	+ dt * sum {i in I diff {0,nt} } ( (x[i,1] - ref1)*(x[i,1] - ref1) 
	                                 + (x[i,2] - ref2)*(x[i,2] - ref2) ) ;
 
subj to ODE_DISC_1 {i in I diff {0}}:
   x[i,1] = x[i-1,1] + dt * ( x[i-1,1] - x[i-1,1]*x[i-1,2] - x[i-1,1]*c1*w[i-1] );
 
subj to ODE_DISC_2 {i in I diff {0}}:
   x[i,2] = x[i-1,2] + dt * ( - x[i-1,2] + x[i-1,1]*x[i-1,2] - x[i-1,2]*c2*w[i-1] );

a data file lotka_ampl.dat,

# ------------------------------------
# Data: Lotka Volterra fishing problem
# ------------------------------------
 
# Algorithmic parameters
param nt := 100;
 
# Problem parameters
param T := 12.0;
param c1 := 0.4;
param c2 := 0.2;
param ref1 := 1.0;
param ref2 := 1.0;
 
# Initial values differential states
let x[0,1] := 0.5;
let x[0,2] := 0.7;
fix x[0,1];
fix x[0,2];
 
# Initial values control
let {i in I} w[i] := 0.0;
fix w[nt];
 
param mysum;

and a running script lotka_ampl.run,

# ----------------------------------------------------
# Solve Lotka Volterra fishing problem via collocation
# ----------------------------------------------------
 
model ampl_lotka.mod;
data ampl_lotka.dat;
 
option solver bonmin;
 
solve;

Variants

There are several alternative formulations and variants of the above problem, in particular

• a prescribed time grid for the control function <bibref>Sager2006</bibref>,
• a time-optimal formulation to get into a steady-state <bibref>Sager2005</bibref>,
• the usage of a different steady-state, as the one corresponding to $w(t) = 1$,
• different fishing control functions for the two species,
• different parameters and start values.

Miscellaneous and Further Reading

The Lotka Volterra fishing problem was introduced by Sebastian Sager in a proceedings paper <bibref>Sager2006</bibref> and revisited in his PhD thesis <bibref>Sager2005</bibref>. These are also the references to look for more details.

References

<bibreferences/>