Bioreactor

The bioreactor example is an easy bioreactor with an substrate that is converted to a product by the biomass in the reactor. It has three states and a control that is describing the feed concentration of substrate. It is taken from the examples folder of the ACADO toolkit described in:

Houska, Boris, Hans Joachim Ferreau, and Moritz Diehl. "ACADO toolkit—An open‐source framework for automatic control and dynamic optimization."
Optimal Control Applications and Methods 32.3 (2011): 298-312.

Originally the problem seems to be motivated by:

VERSYCK, KARINA J., and JAN F. VAN IMPE. "Feed rate optimization for fed-batch bioreactors: From optimal process performance to optimal parameter estimation."
Chemical Engineering Communications 172.1 (1999): 107-124.

Model Formulation

The dynamic model is an ODE model:

$\begin{array}{rcl} \dot{X}&=&-DX+\mu X \\ \dot{S}&=& D(S_{f}-S)-\mu /Y_{xs} X \\ \dot{P}&=&-DP+ (\alpha \mu +\beta) X. \end{array}$

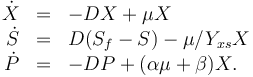
The three states describe the concentration of the biomass (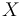$X$), the substrate (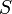$S$), and the product (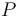$P$) in the reactor. In steady state the feed and outlet are equal and dilute all three concentrations with a ratio 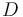$D$. The biomass grows with a rate 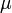$\mu$, while it eats up the substrate with the rate 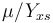$\mu/Y_{xs}$ and produces product at a rate 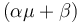$(\alpha \mu +\beta)$. The rate 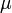$\mu$ is given by:

$\mu = \mu_{m}*(1-P/P_{m})*S/(K_m+S+S^2/K_i)$

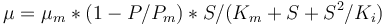
The fixed parameters (constants) of the model are as follows.

Parameters

Name	Symbol	Value	Unit
Dilution	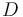$D$	0.15	[-]
Rate coefficient	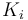$K_i$	22	[-]
Rate coefficient	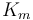$K_m$	1.2	[-]
Rate coefficient	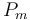$P_m$	50	[-]
Substrate to Biomass rate	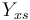$Y_{xs}$	0.4	[-]
Linear slope	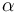$\alpha$	2.2	[-]
Linear intercept	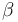$\beta$	0.2	[-]
Maximal growth rate	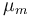$\mu_m$	0.48	[-]

Optimal Control Problem

Writing shortly for the states in vector notation 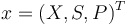$x=(X,S,P)^T$ the OCP reads:

$\begin{array}{cl} \displaystyle \min_{x,S_f} & J(x,S_f)\\[1.5ex] \mbox{s.t.} & \dot{x} = f(x,S_f), \forall \, t \in [0,48]\\ & x(0) = (6.5,12,22)^T \\ & x \in \R^3,\,S_f \in [28.7,40]. \end{array}$

Objective

$J(x,S_f)=\int_0^{48}D(S_f-P)^2dt$

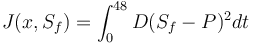
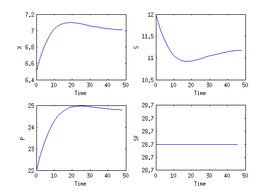
Reference Solution

Here we present the reference solution of the reimplemented example in the ACADO code generation with matlab. The source code is given in the next section.

• Reference solution
• 

  Optimal solution for the ACADO example.

Source Code

In this section one can provide the source code of the implementation, that solved the problem and produced the reference solution. This should be done by providing source files.