Goddart's rocket problem

In Goddart's rocket problem we model the ascent (vertical; restricted to 1 dimension) of a rocket. The aim is to reach a certain altitude with minimal fuel consumption. It is equivalent to maximize the mass at the final altitude.

Variables

The state variables 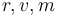$r,v,m$ describe the altitude, speed and mass.

The drag is given by

$D(r,v):= Av^2 \rho(r)\text{, with }\rho(r):= exp(-k\cdot (r-r_0)).$

All units are renormalized.

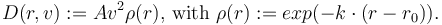
Mathematical formulation

$\begin{array}{llcll} \displaystyle \max_{m,r,v,u,T} & m(T)\\[1.5ex] \mbox{s.t.} & \dot{r} & = & v, \\ & \dot{v} & = & -\frac{1}{r^2} + \frac{1}{m} (T_{max}u-D(r,v)) \\[1.5ex] & \dot{m} & = & -b T_{max} u, \\ & u(\cdot) &\in& [0,1] \\ & r(0) &=& r_0, \\ & v(0) &=& v_0, \\ & m(0) &=& m_0, \\ & r(T) &=& r_T, \\ & D(r(\cdot),v(\cdot))&\le& C \\ & T free \end{array}$

Parameters

$\begin{array}{rcl} r_0 &=& 1 \\ v_0 &=& 0 \\ m_0 &=& 1 \\ r_T &=& 1.01 \\ b &=& 7 \\ T_{max} &=& 3.5 \\ A &=& 310 \\ k &=& 500 \\ \end{array}$