Van der Pol Oscillator (binary variant)
From mintOC
Revision as of 17:42, 10 January 2018 by ClemensZeile (Talk | contribs) (Created page with "{{Dimensions |nd = 1 |nx = 2 |nw = 3 |nre = 2 }}<!-- Do not insert line break here or Dimensions Box moves up in the layout... -->This site describ...")
| Van der Pol Oscillator (binary variant) | |
|---|---|
| State dimension: | 1 |
| Differential states: | 2 |
| Discrete control functions: | 3 |
| Interior point equalities: | 2 |
This site describes a Van der Pol Oscillator variant with three binary controls instead of only one continuous control.
Mathematical formulation
The mixed-integer optimal control problem is given by
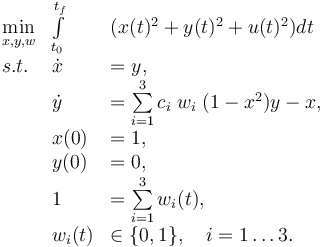
Parameters
These fixed values are used within the model:
![[t_0,t_f]=[0,20], c_1=-1, c_2=0.75, c_3=-2.](https://mintoc.de/images/math/6/5/5/6556b72c5eff2a3dcb8b0c40da03d1fd.png)
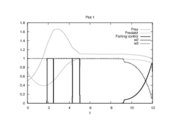
Reference Solutions
If the problem is relaxed, i.e., we demand that 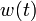 be in the continuous interval
be in the continuous interval ![[0, 1]](https://mintoc.de/images/math/c/c/f/ccfcd347d0bf65dc77afe01a3306a96b.png) instead of the binary choice
instead of the binary choice 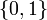 , the optimal solution can be determined by means of direct optimal control.
, the optimal solution can be determined by means of direct optimal control.
The optimal objective value of the relaxed problem with 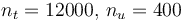 is
is 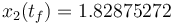 . The objective value of the binary controls obtained by Combinatorial Integral Approimation (CIA) is
. The objective value of the binary controls obtained by Combinatorial Integral Approimation (CIA) is 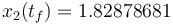 .
.
- Reference solution plots