Control of Heat Equation with Actuator Placement
| Control of Heat Equation with Actuator Placement | |
|---|---|
| State dimension: | 1 |
| Differential states: | 1 |
| Continuous control functions: |
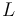 |
| Discrete control functions: |
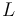 |
| Path constraints: | 3 |
| Interior point equalities: | 2 |
This problem is governed by the heat equation and is adapted from Iftime and Demetriou ([Iftime2009]Author: Orest V. Iftime; Michael A. Demetriou
Journal: {A}utomatica
Number: 2
Pages: 312--323
Title: {O}ptimal control of switched distributed parameter systems with spatially scheduled actuators
Volume: 45
Year: 2009 ).
Its goal is to choose a place to apply an actuator in a given area depending on time.
We consider a rectangle
).
Its goal is to choose a place to apply an actuator in a given area depending on time.
We consider a rectangle ![\Omega=[0,1]\times[0,2]](https://mintoc.de/images/math/b/9/e/b9e9ecbd1ca99669f6d13a62bcf6142b.png) with the boundary
with the boundary 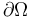 and the time horizon
and the time horizon ![T=[0,10]](https://mintoc.de/images/math/0/a/e/0aef63dc3199780b7093eeb4bd8d74f5.png) as the domains.
The objective function is quadratic, its first term captures the desired final state
as the domains.
The objective function is quadratic, its first term captures the desired final state 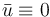 , the second term regularize the state over time and the third term regularize the continuous controls.
The constraints are a source budget, which limits the quantity of placed actuators, and the two-dimensional heat equation with some source function.
Additionally, we assume Dirichlet boundary conditions and initial conditions.
, the second term regularize the state over time and the third term regularize the continuous controls.
The constraints are a source budget, which limits the quantity of placed actuators, and the two-dimensional heat equation with some source function.
Additionally, we assume Dirichlet boundary conditions and initial conditions.
Mathematical formulation
Parameters
Reference solution
Source Code
References
| [Iftime2009] | Orest V. Iftime; Michael A. Demetriou (2009): {O}ptimal control of switched distributed parameter systems with spatially scheduled actuators . {A}utomatica, 45, 312--323 |  |