Lotka Volterra fishing problem

This problem was set up as a simple benchmark problem. Despite of its simple structure, the optimal solution contains a singular arcs, making the Lotka Volterra fishing problem an ideal candidate for benchmarking of algorithms.

In this problem the Lotka Volterra equations for a predator-prey system have been augmented by an additional linear term, relating to fishing by man.

Model dimensions and properties

The model has the following dimensions:

$\begin{array}{rcl} n_x &=& 3\\ n_z &=& 0\\ n_u &=& 0\\ n_w &=& 1\\ n_p &=& 0\\ n_{\rho} &=& 0\\ n_c &=& 0\\ n_{r^\mathrm{i}} &=& 0\\ n_{r^\mathrm{e}} &=& 3 \end{array}$

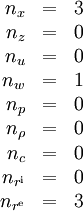
It is thus an ODE model with a single integer control function. The interior point equality conditions fix the initial values of the differential states.

Mathematical formulation

For $t \in [t_0, t_f]$ the mixed-integer optimal control problem is given by

$\begin{array}{llcl} \displaystyle \min_{x, w} & x_2(t_f) \\[1.5ex] \mbox{s.t.} & \dot{x}_0(t) & = & x_0(t) - x_0(t) x_1(t) - \; c_0 x_0(t) \; w(t), \\ & \dot{x}_1(t) & = & - x_1(t) + x_0(t) x_1(t) - \; c_1 x_1(t) \; w(t), \\ & \dot{x}_2(t) & = & (x_0(t) - 1)^2 + (x_1(t) - 1)^2, \\[1.5ex] & x(0) &=& x_0, \\ & w(t) &\in& \{0, 1\}. \end{array}$

Initial values and parameters

$\begin{array}{rcl} t_0 &=& 0\\ t_f &=& 12\\ c_0 &=& 0.4\\ c_1 &=& 0.2\\ x_0 &=& (0.5, 0.7, 0)^T \end{array}$

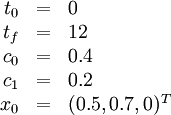
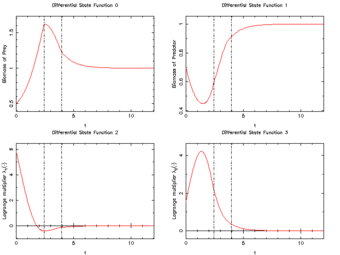
Reference Solutions

States

The two differential states and corresponding adjoint variables in the indirect approach

Source Code

  double ref0 = 1, ref1 = 1;                 /* steady state with u == 0 */

  rhs[0] =   xd[0] - xd[0]*xd[1] - p[0]*u[0]*xd[0];
  rhs[1] = - xd[1] + xd[0]*xd[1] - p[1]*u[0]*xd[1];
  rhs[2] = (xd[0]-ref0)*(xd[0]-ref0) + (xd[1]-ref1)*(xd[1]-ref1);

Miscellaneous

Testing Graphviz

<graphviz border='frame' format='svg'> digraph G {Hello->World!} </graphviz>

Testing Syntax Highlighting

// Hello World in Microsoft C# ("C-Sharp").
 
using System;
 
class HelloWorld
{
    public static int Main(String[] args)
    {
        Console.WriteLine("Hello, World!");
        return 0;
    }
}