Lotka Volterra fishing problem (APMonitor)
From mintOC
Revision as of 23:03, 20 November 2017 by JohnHedengren (Talk | contribs) (APMontor solution of Volterra fishing problem)
This page contains a solution of the MIOCP Lotka Volterra fishing problem in APMonitor Python format. A MATLAB version is also available from the Dynamic Optimization Course as Example 3 (lotka_volterra_fishing.zip).
APMonitor
The model in Python code for a fixed control discretization grid using orthogonal collocation and a simultaneous optimization method. The APMonitor package is available with pip install APMonitor or from the APMonitor Python Github repository.
import numpy as np import matplotlib.pyplot as plt # retrieve apm.py from # https://raw.githubusercontent.com/APMonitor/apm_python/master/apm.py # or # http://apmonitor.com/wiki/index.php/Main/PythonApp # from apm import * # pip install with 'pip install APMonitor' from APMonitor.apm import * # local APMonitor servers are available for Windows or Linux # http://apmonitor.com/wiki/index.php/Main/APMonitorServer # with clients in Python, MATLAB, and Julia # write model model = ''' ! apopt MINLP solver options (see apopt.com) File apopt.opt minlp_maximum_iterations 1000 ! minlp iterations minlp_max_iter_with_int_sol 50 ! minlp iterations if integer solution is found minlp_as_nlp 0 ! treat minlp as nlp nlp_maximum_iterations 200 ! nlp sub-problem max iterations minlp_branch_method 1 ! 1 = depth first, 2 = breadth first minlp_gap_tol 0.001 ! covergence tolerance minlp_integer_tol 0.001 ! maximum deviation from whole number to be considered an integer minlp_integer_leaves 0 ! create soft (1) integer leaves or hard (2) integer leaves with branching End File Constants c0 = 0.4 c1 = 0.2 Parameters last Variables x0 = 0.5 , >= 0 x1 = 0.7 , >= 0 x2 = 0.0 , >= 0 int_w = 0 , >= 0 , <= 1 Intermediates w = int_w Equations minimize last * x2 $x0 = x0 - x0*x1 - c0*x0*w $x1 = - x1 + x0*x1 - c1*x1*w $x2 = (x0-1)^2 + (x1-1)^2 ''' fid = open('lotka_volterra.apm','w') fid.write(model) fid.close() # write data file time = np.linspace(0,12,121) time = np.insert(time, 1, 0.01) last = np.zeros(122) last[-1] = 1.0 data = np.vstack((time,last)) np.savetxt('data.csv',data.T,delimiter=',',header='time,last',comments='') # specify server and application name s = 'http://byu.apmonitor.com' #s = 'http://127.0.0.1/' # for local APMonitor server a = 'lotka' apm(s,a,'clear all') apm_load(s,a,'lotka_volterra.apm') csv_load(s,a,'data.csv') apm_option(s,a,'nlc.imode',6) # Nonlinear control / dynamic optimization apm_option(s,a,'nlc.nodes',3) apm_info(s,a,'MV','int_w') # M or MV = Manipulated variable - independent variable over time horizon apm_option(s,a,'int_w.status',1) # Status: 1=ON, 0=OFF apm_option(s,a,'int_w.mv_type',0) # MV Type = Zero Order Hold apm_option(s,a,'nlc.solver',1) # 1 = APOPT # solve output = apm(s,a,'solve') print(output) # retrieve solution y = apm_sol(s,a) plt.figure(1) plt.step(y['time'],y['int_w'],'r-',label='w (0/1)') plt.plot(y['time'],y['x0'],'b-',label=r'$x_0$') plt.plot(y['time'],y['x1'],'k-',label=r'$x_1$') plt.plot(y['time'],y['x2'],'g-',label=r'$x_2$') plt.xlabel('Time') plt.ylabel('Variables') plt.legend(loc='best') plt.show()
Results
IPOPT
The relaxed solution calculated by IPOPT (Ipopt 3.12, Linux x86_64, default settings, 4 GHz quadcore, Linux 4.2.0-23-generic) has an objective function value of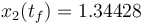 
. IPOPT requires 22 iterations (6.062 seconds of processing time). The following is a Gnuplot compatible tabular version of the solution:
# t, x_0, x_1, u
0, 0.5, 0.7, 5.18436e-09
0.12, 0.519594, 0.659989, 5.42459e-09
0.24, 0.542429, 0.623852, 5.79496e-09
0.36, 0.568601, 0.591429, 6.30563e-09
0.48, 0.59823, 0.562571, 6.97415e-09
0.6, 0.631456, 0.537143, 7.827e-09
0.72, 0.66843, 0.515028, 8.90236e-09
0.84, 0.709312, 0.496134, 1.02545e-08
0.96, 0.75426, 0.480401, 1.19611e-08
1.08, 0.803421, 0.4678, 1.41346e-08
1.2, 0.856919, 0.458344, 1.69417e-08
1.32, 0.914842, 0.452091, 2.06377e-08
1.44, 0.97722, 0.449154, 2.56285e-08
1.56, 1.044, 0.449708, 3.2592e-08
1.68, 1.11503, 0.454003, 4.27322e-08
1.8, 1.18998, 0.462372, 5.83658e-08
1.92, 1.26837, 0.475251, 8.44574e-08
2.04, 1.34942, 0.493189, 1.33425e-07
2.16, 1.43209, 0.516862, 2.44977e-07
2.28, 1.51492, 0.547087, 6.24464e-07
2.4, 1.59605, 0.584816, 0.715281
2.52, 1.61776, 0.61833, 0.999999
2.64, 1.61116, 0.6499, 0.999999
2.76, 1.59844, 0.68229, 1
2.88, 1.57963, 0.714939, 1
3, 1.55497, 0.747196, 1
3.12, 1.52487, 0.778343, 0.999999
3.24, 1.48993, 0.807625, 0.999999
3.36, 1.4509, 0.83429, 0.999999
3.48, 1.40865, 0.857635, 0.999998
3.6, 1.36412, 0.877047, 0.999997
3.72, 1.31827, 0.892039, 0.999991
3.84, 1.27203, 0.90228, 0.999646
3.96, 1.22628, 0.907616, 0.536112
4.08, 1.20755, 0.919653, 0.581667
4.2, 1.18502, 0.928525, 0.503883
4.32, 1.16606, 0.936899, 0.464153
4.44, 1.14851, 0.944178, 0.418428
4.56, 1.13278, 0.950658, 0.378617
4.68, 1.11859, 0.956378, 0.341493
4.8, 1.10582, 0.961433, 0.3073
4.92, 1.09438, 0.965904, 0.276462
5.04, 1.08411, 0.969849, 0.248219
5.16, 1.07492, 0.973333, 0.222481
5.28, 1.0667, 0.976412, 0.19935
5.4, 1.05936, 0.97913, 0.178262
5.52, 1.0528, 0.981533, 0.159402
5.64, 1.04696, 0.983656, 0.142349
5.76, 1.04175, 0.985532, 0.127041
5.88, 1.0371, 0.987191, 0.1133
6, 1.03297, 0.988657, 0.100985
6.12, 1.02929, 0.989954, 0.0899604
6.24, 1.02601, 0.991101, 0.0800981
6.36, 1.0231, 0.992117, 0.0712934
6.48, 1.02051, 0.993015, 0.0634308
6.6, 1.01821, 0.993811, 0.0564127
6.72, 1.01617, 0.994515, 0.0501573
6.84, 1.01435, 0.995139, 0.0445824
6.96, 1.01274, 0.995691, 0.0396177
7.08, 1.01131, 0.99618, 0.0351979
7.2, 1.01003, 0.996613, 0.0312714
7.32, 1.0089, 0.996997, 0.027765
7.44, 1.0079, 0.997337, 0.0246626
7.56, 1.00701, 0.997639, 0.0218975
7.68, 1.00622, 0.997905, 0.0194423
7.8, 1.00552, 0.998142, 0.0172603
7.92, 1.0049, 0.998351, 0.0153224
8.04, 1.00435, 0.998537, 0.0136015
8.16, 1.00386, 0.998701, 0.0120735
8.28, 1.00342, 0.998847, 0.0107171
8.4, 1.00303, 0.998976, 0.00951328
8.52, 1.00269, 0.99909, 0.00844491
8.64, 1.00239, 0.999191, 0.00749702
8.76, 1.00212, 0.999281, 0.00665598
8.88, 1.00188, 0.99936, 0.00590975
9, 1.00167, 0.99943, 0.00524776
9.12, 1.00148, 0.999492, 0.00466052
9.24, 1.00131, 0.999547, 0.00413914
9.36, 1.00117, 0.999596, 0.00367206
9.48, 1.00103, 0.999637, 0.00326159
9.6, 1.00092, 0.999675, 0.00290302
9.72, 1.00082, 0.999707, 0.00258504
9.84, 1.00072, 0.999736, 0.00230262
9.96, 1.00064, 0.999762, 0.00205186
10.08, 1.00057, 0.999785, 0.00182951
10.2, 1.00051, 0.999805, 0.00163302
10.32, 1.00045, 0.999822, 0.00146039
10.44, 1.0004, 0.999838, 0.00131011
10.56, 1.00036, 0.999851, 0.00118097
10.68, 1.00032, 0.999863, 0.00107188
10.8, 1.00028, 0.999872, 0.000981659
10.92, 1.00025, 0.99988, 0.00090944
11.04, 1.00022, 0.999886, 0.000854893
11.16, 1.00019, 0.99989, 0.000818284
11.28, 1.00017, 0.999892, 0.000801181
11.4, 1.00014, 0.999891, 0.000807844
11.52, 1.00012, 0.999886, 0.000848734
11.64, 1.00009, 0.999878, 0.000951928
11.76, 1.00006, 0.999864, 0.00121852
11.88, 1.00002, 0.999838, 0.00267036
12, 0.999915, 0.999769, 0
