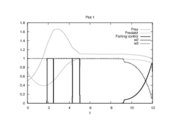
Lotka Volterra absolute fishing problem

Lotka Volterra absolute fishing problem
State dimension:	1
Differential states:	3
Discrete control functions:	5
Interior point equalities:	3

This site describes a Lotka Volterra variant with five binary controls that all represent fishing of an absolute biomass.

Mathematical formulation

The mixed-integer optimal control problem is given by

$\begin{array}{llclr} \displaystyle \min_{x, w} & x_2(t_f) \\[1.5ex] \mbox{s.t.} & \dot{x}_0 & = & x_0 - x_0 x_1 - \; \sum\limits_{i=1}^{5} c_{0,i}\; w_i, \\ & \dot{x}_1 & = & - x_1 + x_0 x_1 - \; \sum\limits_{i=1}^{5} c_{1,i}\; w_i, \\ & \dot{x}_2 & = & (x_0 - 1)^2 + (x_1 - 1)^2, \\[1.5ex] & x(0) &=& (0.5, 0.7, 0)^T, \\ & \sum\limits_{i=1}^{5}w_i(t) &=& 1, \\ & w_i(t) &\in& \{0, 1\}, \quad i=1\ldots 5. \end{array}$

Here the differential states 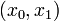$(x_0, x_1)$ describe the biomasses of prey and predator, respectively. The third differential state is used here to transform the objective, an integrated deviation, into the Mayer formulation 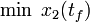$\min \; x_2(t_f)$. This problem variant allows to choose between three different fishing options.

Parameters

These fixed values are used within the model.

$\begin{array}{rcl} [t_0, t_f] &=& [0, 12],\\ (c_{0,1}, c_{1,1}) &=& (0.2, 0.1),\\ (c_{0,2}, c_{1,2}) &=& (0.4, 0.2),\\ (c_{0,3}, c_{1,3}) &=& (0.01, 0.1),\\ (c_{0,4}, c_{1,4}) &=& (0, 0),\\ (c_{0,5}, c_{1,5}) &=& (-0.1, -0.2). \end{array}$

Reference Solutions

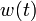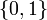If the problem is relaxed, i.e., we demand that $w(t)$ be in the continuous interval $[0, 1]$ instead of the binary choice $\{0,1\}$, the optimal solution can be determined by means of direct optimal control.

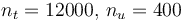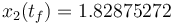The optimal objective value of the relaxed problem with $n_t=12000, \, n_u=400$ is $x_2(t_f) =1.82875272$. The objective value of the binary controls obtained by Combinatorial Integral Approimation (CIA) is $x_2(t_f) =1.82878681$.

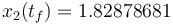• Reference solution plots
• 

  Optimal relaxed controls and states determined by an direct approach with ampl_mintoc (Radau collocation) and $n_t=12000, \, n_u=400$.

• 

  Optimal binary controls and states determined by an direct approach (Radau collocation) with ampl_mintoc and $n_t=12000, \, n_u=400$. The relaxed controls were approximated by Combinatorial Integral Approximation.