Car testdrive (lane change manoeuvre)
| Car testdrive (lane change manoeuvre) | |
|---|---|
| State dimension: | 1 |
| Differential states: | 7 |
| Continuous control functions: | 3 |
| Discrete control functions: | 1 |
| Interior point equalities: | 7 |
The mathematical equations form a small-scale ODE model.
Contents
[hide]Mathematical formulation
For ![t \in [t_0, t_f]](https://mintoc.de/images/math/5/5/8/55823791d9100bcb5461801aff4f6edd.png) almost everywhere the mixed-integer optimal control problem is given by
almost everywhere the mixed-integer optimal control problem is given by
![\begin{array}{llcl}
\displaystyle \min_{x, w} & t_f \\[1.5ex]
\mbox{s.t.} & \dot{x}(t) & = & f( x(t), u(t), \mu(t)), \\
& x(0) &=& x_0, \\
& \mu(t) &\in& \{1, 2, 3, 4, 5\}.
\end{array}](https://mintoc.de/images/math/d/6/7/d67761ea91b7564ff5cb091f6fef15f4.png)
Parameters
These fixed values are used within the model.

Test course
The double-lane change manoeuvre presented in <bibref>Gerdts2005</bibref> is realized by constraining the car's position onto a prescribed track at any time ![t\in[t_0,t_\text{f}]](https://mintoc.de/images/math/e/2/3/e234c61ce225d19679331caf0281c8b0.png) . Starting in the left position with an initial prescribed velocity, the driver is asked to manage a change of lanes modeled by an offset of 3.5 meters in the track. Afterwards he is asked to return to the starting lane. This manoeuvre can be regarded as an overtaking move or as an evasive action taken to avoid hitting an obstacle suddenly appearing on the starting lane.
. Starting in the left position with an initial prescribed velocity, the driver is asked to manage a change of lanes modeled by an offset of 3.5 meters in the track. Afterwards he is asked to return to the starting lane. This manoeuvre can be regarded as an overtaking move or as an evasive action taken to avoid hitting an obstacle suddenly appearing on the starting lane.
From a mathematical point of view, the test track is described by setting up piecewise cubic spline functions 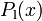 and
and 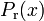 modeling the top and bottom track boundary, given a horizontal position
modeling the top and bottom track boundary, given a horizontal position 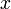 .
.
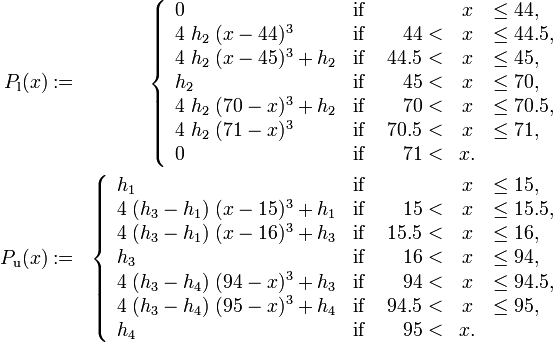
where 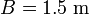 is the car's width and
is the car's width and
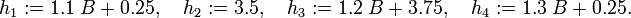
Reference Solutions
Reference solutions for the case of a fixed time-grid are given in <bibref>Gerdts2005</bibref>. Solutions for a non-fixed time grid are given in <bibref>Gerdts2006</bibref>.
Source Code
C
Variants
See testdrive overview page.
References
<bibreferences/>