Fuller's problem
| Fuller's problem | |
|---|---|
| State dimension: | 1 |
| Differential states: | 2 |
| Discrete control functions: | 1 |
| Interior point equalities: | 4 |
The first control problem with an optimal chattering solution was given by <bibref>Fuller1963</bibref>. An optimal trajectory does exist for all initial and terminal values in a vicinity of the origin. As Fuller showed, this optimal trajectory contains a bang-bang control function that switches infinitely often.
The mathematical equations form a small-scale ODE model. The interior point equality conditions fix initial and terminal values of the differential states.
Contents
[hide]Mathematical formulation
For ![t \in [t_0, t_f]](https://mintoc.de/images/math/5/5/8/55823791d9100bcb5461801aff4f6edd.png) almost everywhere the mixed-integer optimal control problem is given by
almost everywhere the mixed-integer optimal control problem is given by
![\begin{array}{llcl}
\displaystyle \min_{x, w} & \int_{0}^{1} x_0^2 \; \mathrm{d} t \\[1.5ex]
\mbox{s.t.} & \dot{x}_0(t) & = & x_1(t), \\
& \dot{x}_1(t) & = & 1 - 2 \; w(t), \\[1.5ex]
& x(0) &=& x_S, \\
& x(t_f) &=& x_T, \\
& w(t) &\in& \{0, 1\}.
\end{array}](https://mintoc.de/images/math/b/c/8/bc817f0912abd1c57882137cc7ea7a5d.png)
Parameters
We use 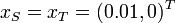 .
.
Reference Solutions
Source Code
The solution found for the relaxed Fuller's problem with optimica using the solver Ipopt (with the linear solver MA27) is obtained with 12 iterations and the objective is 1.5296058259296967e-05.
The differential equations in C code:
Miscellaneous and further reading
An extensive analytical investigation of this problem and a discussion of the ubiquity of Fuller's problem can be found in <bibref>Zelikin1994</bibref>, a recent investigation of chattering controls in relay feedback systems in <bibref>Johansson2002</bibref>.
References
<bibreferences/>
