Bang-bang approximation of a traveling wave

The following problem is an academic example of a PDE constrained optimal control problem with integer control constraints.

The control task consists of choosing the boundary value of a transport equation from the extremal values of a traveling wave such that the 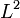$L^2$-distance between the traveling wave and the resulting flow is minimized.

Mathematical formulation

$\begin{array}{ll} \displaystyle \min_{x, q} & \displaystyle \int_0^1\int_0^1 |x(t,s)-x_d(t,s)|^2\,ds\,dt + c \bigvee_0^1 q(t)\,dt \\[1.5ex] \mbox{s.t.} & \displaystyle \frac{\partial}{\partial t}x(t,s)+\frac{\partial}{\partial s}x(t,s) = 0,\quad 0<s<1,~0<t<1\\[1.5ex] & \displaystyle x(t,0) = q(t),\quad 0<t<1 \\ & \displaystyle x(0,s) = x_d(0,s),\quad 0<s<1 \\ & \displaystyle q(t) \in \{0,1\},\quad 0<t<1 \\ \end{array}$

where

$x_d(t,s)=\frac12\sin(5\pi(t-s))+1,\quad 0\leq t \leq 1,~0\leq s\leq 1$

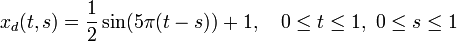
is the traveling wave (oscillating between 0 and 1), 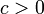$c>0$ is a (small) regularization parameter and 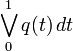$\bigvee_0^1 q(t)\,dt$ denotes the variation of q(\cdot) over the interval $[0,1]$. Thereby, the solution of the transport equation has to be understood in the usual weak sense defined by the characteristic equations.

References

<bibreferences/>