Bioreactor

The bioreactor example is an easy bioreactor with an enzyme-substrate reaction. It has three states and a control that is describing the feed concentration of substrate. It is taken from the examples folder of the ACADO toolkit described in:

Houska, Boris, Hans Joachim Ferreau, and Moritz Diehl. "ACADO toolkit—An open‐source framework for automatic control and dynamic optimization."
Optimal Control Applications and Methods 32.3 (2011): 298-312.

Model Formulation

The dynamic model is an ODE model:

Failed to parse (syntax error): \dot{X}=-DX+\mu X \\ \dot{S}= D(Sf-S)-\mu/Y_{xs} X \\ \dot{P}=-DP+ (\alpha \mu+\beta) X

In this section the dynamic model, that describes the physical or technical process of interest, should be described. First the differential equation should be written down. Then the states, inputs, and parameters should be declared (Dimension, Type (integer, real, binary, ...)). Finally the parameters that are not free in the optimization and the coefficients should be stated in an extra table or list. All equations and functions are defined over an interval 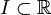$I \subset \R$. Initial values and free parameters are taken into account later in the Optimal Control Problem.

Ordinary Differential Equation

For a simple scalar ODE model this would look like the following:

$\dot{x}=px+u,\; \forall \, t \in I;\; x: I \rightarrow \R,\; u: I \rightarrow \R, \; p \in \R.$

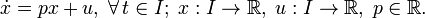
The parameter (coefficient) 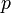$p$ could be stated in a table, if it is fixed.

Parameter(s)

Name	Symbol	Value	Unit
Parameter	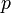$p$	23	[-]

This would result in an right hand side function 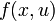$f(x,u)$ in this case, because there are no free parameters. Of course one could also specify an implicit DAE system (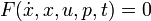$F(\dot{x},x,u,p,t)=0$), where it just hast to be said which states are differential and which are algebraic.