Batch reactor (GEKKO)

This page contains a solution of the Batch reactor problem in GEKKO Python format. The model in Python code for a fixed control discretization grid uses orthogonal collocation and a simultaneous optimization method. The GEKKO package is available with pip install gekko.

import numpy as np
import matplotlib.pyplot as plt
from gekko import GEKKO
 
m = GEKKO()
 
nt = 501
m.time = np.linspace(0,1,nt)
 
# Variables
x1 = m.Var(value=1)
x2 = m.Var(value=0)
T = m.MV(value=398,lb=298,ub=398)
T.STATUS = 1
T.DCOST = 1e-6
k1 = m.Intermediate(4000*m.exp(-2500/T))
k2 = m.Intermediate(6.2e5*m.exp(-5000/T))
 
p = np.zeros(nt)
p[-1] = 1.0
final = m.Param(value=p)
 
# Equations
m.Equation(x1.dt()==-k1*x1**2)
m.Equation(x2.dt()==k1*x1**2 - k2*x2)
 
# Objective Function
# maximize final x2
m.Obj(-x2*final)
 
m.options.IMODE = 6
m.options.NODES = 3
m.solve()
 
print('Optimal x2(tf): ' + str(x2.value[-1]))
 
plt.figure(1)
plt.subplot(2,1,1)
plt.plot(m.time,x1.value,'k:',\
         LineWidth=2,label=r'$x_1$')
plt.plot(m.time,x2.value,'b-',\
         LineWidth=2,label=r'$x_2$')
plt.plot(m.time[-1],x2.value[-1],'o',\
         color='orange',MarkerSize=5,\
         label=r'$x_2\left(t_f\right)$')
plt.legend()
plt.ylabel('Mole Fraction')
plt.subplot(2,1,2)
plt.plot(m.time,T.value,'r--',\
         LineWidth=2,label='Temperature')
plt.ylabel(r'$T/;(^oC)$')
plt.legend(loc='best')
plt.xlabel('Time')
plt.ylabel('Value')
plt.show()

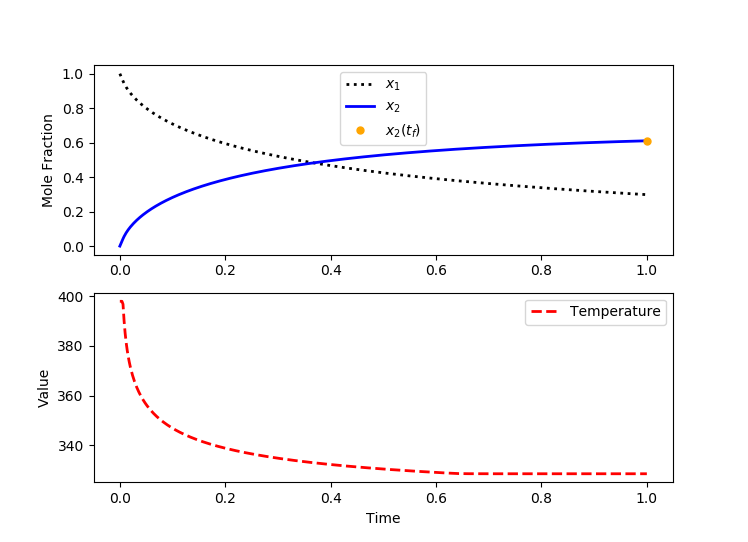
A solution is calculated with an objective function value of x2(tf) = 0.6108.