Category:Complementarity constraints
This category contains optimization problems with complementarity constraints (MPCCs), for generic variables / functions 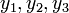 in the form of
in the form of
![\begin{array}{llcl}
\displaystyle \min_{y_1, y_2, y_3} & & & \Phi(y_1, y_2, y_3) \\[1.5ex]
\mbox{s.t.} & 0 & = & F ( y_1, y_2, y_3), \\
& 0 & \le & C ( y_1, y_2, y_3), \\
& 0 & \le & y_1 \perp y_2 \ge 0,
\end{array}](https://mintoc.de/images/math/a/4/1/a41c1faf8271852a05aaba326dd240ef.png)
The complementarity operator 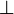 implies the disjunctive behavior
implies the disjunctive behavior
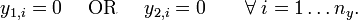
MPCCs may arise from a reformulation of a bilevel optimization problem by writing the optimality conditions of the inner problem as variational constraints of the outer optimization problem, or from a special treatment of state-dependent switches, [Baumrucker2009]Author: B.T. Baumrucker; L.T. Biegler
Journal: Journal of Process Control
Note: Special Section on Hybrid Systems: Modeling, Simulation and Optimization
Number: 8
Pages: 1248--1256
Title: MPEC strategies for optimization of a class of hybrid dynamic systems
Volume: 19
Year: 2009 . Note that all MPCCs can be reformulated as MPECs.
. Note that all MPCCs can be reformulated as MPECs.
References
| [Baumrucker2009] | B.T. Baumrucker; L.T. Biegler (2009): MPEC strategies for optimization of a class of hybrid dynamic systems. Journal of Process Control, 19, 1248--1256 |  |
This category currently contains no pages or media.