Category:Equilibrium constraints
From mintOC
This category contains mathematical programs with equilibrium constraints (MPECs). An MPEC is an optimization problem constrained by a variational inequality, which takes for generic variables / functions 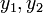 the following general form:
the following general form:
![\begin{array}{llcl}
\displaystyle \min_{y_1, y_2, y_3} & & & \Phi(y_1, y_2, y_3) \\[1.5ex]
\mbox{s.t.} & 0 & = & F ( y_1, y_2, y_3), \\
& 0 & \le & C ( y_1, y_2, y_3), \\
& 0 & \le & (\mu - y_2)^T \; \phi( y_1, y_2), \; y_2 \in Y(y_1), \; \forall \mu \in Y(y_1),
\end{array}](https://mintoc.de/images/math/f/4/d/f4d20f04f516a6ae8307a4f50497aed6.png)
where 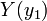 is the feasible region for the variational inequality and given function
is the feasible region for the variational inequality and given function 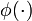 . Variational inequalities arise in many domains and are generally referred to as equilibrium constraints. The variables
. Variational inequalities arise in many domains and are generally referred to as equilibrium constraints. The variables 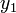 and
and 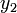 may be controls or states.
may be controls or states.
Complementarity constraints and vanishing constraints are special cases.
This category currently contains no pages or media.