Difference between revisions of "Control of Heat Equation with Actuator Placement"

From mintOC
Jump to: navigation, search
(→‎Parameters)
(→‎Parameters)
Line 45: Line 45:
 
\begin{array}{rcl}
 
\begin{array}{rcl}
 
L &=& 9, \\
 
L &=& 9, \\
−
\kappa &=& 0.01.
+
\kappa &=& 0.01,\\
 +
t_f &=&10.
 
\end{array}
 
\end{array}
 
</math>
 
</math>
  
 
The  parameter  <math> \kappa </math> describes the thermal dissipativity of the material in the domain <math> \Omega </math>, it may vary in space.
 
The  parameter  <math> \kappa </math> describes the thermal dissipativity of the material in the domain <math> \Omega </math>, it may vary in space.
−
The parameter  <math> L </math> indicates the number of possible actuator locations. They are distributed as indecated inthe picture.
+
The parameter  <math> L </math> indicates the number of possible actuator locations. They are distributed as indecated in the picture.
−
 
+
−
\begin{figure}[h]
+
−
  \centering
+
−
  \begin{tikzpicture}
+
−
  \draw[step=1cm] (0,0) grid (8,4);
+
−
  \filldraw[blue] (2,1) circle (4pt);
+
−
  \filldraw[blue] (4,1) circle (4pt);
+
−
  \filldraw[blue] (6,1) circle (4pt);
+
−
  \filldraw[blue] (2,2) circle (4pt);
+
−
  \filldraw[blue] (4,2) circle (4pt);
+
−
  \filldraw[blue] (6,2) circle (4pt);
+
−
  \filldraw[blue] (2,3) circle (4pt);
+
−
  \filldraw[blue] (4,3) circle (4pt);
+
−
  \filldraw[blue] (6,3) circle (4pt);
+
−
  \end{tikzpicture}
+
−
\end{figure}
+
  
 
==Reference solution==
 
==Reference solution==

Revision as of 17:41, 23 February 2016

Control of Heat Equation with Actuator Placement
State dimension: 1
Differential states: 1
Continuous control functions: L
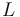Discrete control functions: L
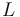Path constraints: 3
Interior point equalities: 2


This problem is governed by the heat equation and is adapted from Iftime and Demetriou ([Iftime2009]Author: Orest V. Iftime; Michael A. Demetriou
Journal: {A}utomatica
Number: 2
Pages: 312--323
Title: {O}ptimal control of switched distributed parameter systems with spatially scheduled actuators
Volume: 45
Year: 2009
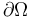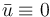Link to Google Scholar). Its goal is to choose a place to apply an actuator in a given area depending on time. We consider a rectangle \Omega=[0,1]\times[0,2] with the boundary \partial\Omega and the time horizon T=[0,10] as the domains. The objective function is quadratic, its first term captures the desired final state \bar{u}\equiv 0, the second term regularize the state over time and the third term regularize the continuous controls. The constraints are a source budget, which limits the quantity of placed actuators, and the two-dimensional heat equation with some source function. Additionally, we assume Dirichlet boundary conditions and initial conditions.


Mathematical formulation

\begin{array}{llcl} \min\limits_{u,v,w}~~ &J(u,v)=||u(\cdot,\cdot,10)||_{2,\Omega}^2 +2||u(\cdot,\cdot,\cdot)||_{2,\Omega\times T}^2+\frac{1}{500}\sum\limits_{l=1}^L||v_l(\cdot)||^2_{2,T} & \\[10pt] \text{ s.t.} ~~~~ &\frac{\partial u}{\partial t}(x,y,t)- \kappa \Delta u(x,y,t)=\sum\limits_{l=1}^9 v_l(t) f_l(x,y) &\text{ in }&\Omega\times T\\[10pt] & u(x,y,t) =0 &\text{ on } &\partial\Omega\times T \\[10pt] & u(x,y,0) = 100 \sin(\pi x)\sin(\pi y) &\text{ in }& \Omega\\[10pt] & -M w_l(t)\leq v_l(t)\leq M w_l(t) \text{ for all } l\in \{1,\dots,L\} &\text{ in } & T \\[10pt] & \sum\limits_{l=1}^L w_l(t) = 1 &\text{ in } & T\\[10pt] & w_l(t)\in \{0,1\} \text{ for all } l\in \{1,\dots,L\} &\text{ in } &T. \end{array}

Parameters

These fixed values are used within the model.

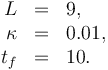
\begin{array}{rcl} L &=& 9, \\ \kappa &=& 0.01,\\ t_f &=&10. \end{array}

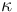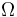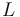The parameter \kappa describes the thermal dissipativity of the material in the domain \Omega , it may vary in space. The parameter L indicates the number of possible actuator locations. They are distributed as indecated in the picture.

Reference solution

Source Code

References

[Iftime2009]Orest V. Iftime; Michael A. Demetriou (2009): {O}ptimal control of switched distributed parameter systems with spatially scheduled actuators . {A}utomatica, 45, 312--323Link to Google Scholar
Retrieved from "https://mintoc.de/index.php?title=Control_of_Heat_Equation_with_Actuator_Placement&oldid=1789"